Mathematics
In triangle ABC, ∠BAC = 90° and AD is perpendicular to side BC. Triangle ABD is similar to triangle CBA by :
SAS
ASA
AAA
RHS
Similarity
35 Likes
Answer
In △ CBA and △ ABD,

⇒ ∠CAB = ∠ADB (Both equal to 90°)
⇒ ∠CBA = ∠DBA (Common angles)
Since, two angles of two triangles are equal so third angle of both the triangle will also be equal.
⇒ ∠ACB = ∠DAB.
∴ △ CBA ~ △ ABD (By A.A.A. postulate)
Hence, Option 3 is the correct option.
Answered By
18 Likes
Related Questions
In the given figure, Δ ABC and Δ DEF are similar, BM and EN are their medians. If Δ ABC is similar to Δ DEF, prove that :
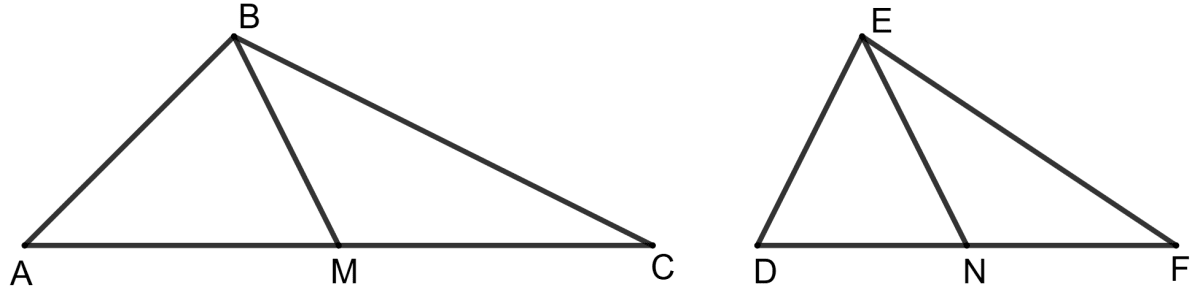
(i) Δ AMB ∼ Δ DNE
(ii) Δ CMB ∼ Δ FNE
(iii)
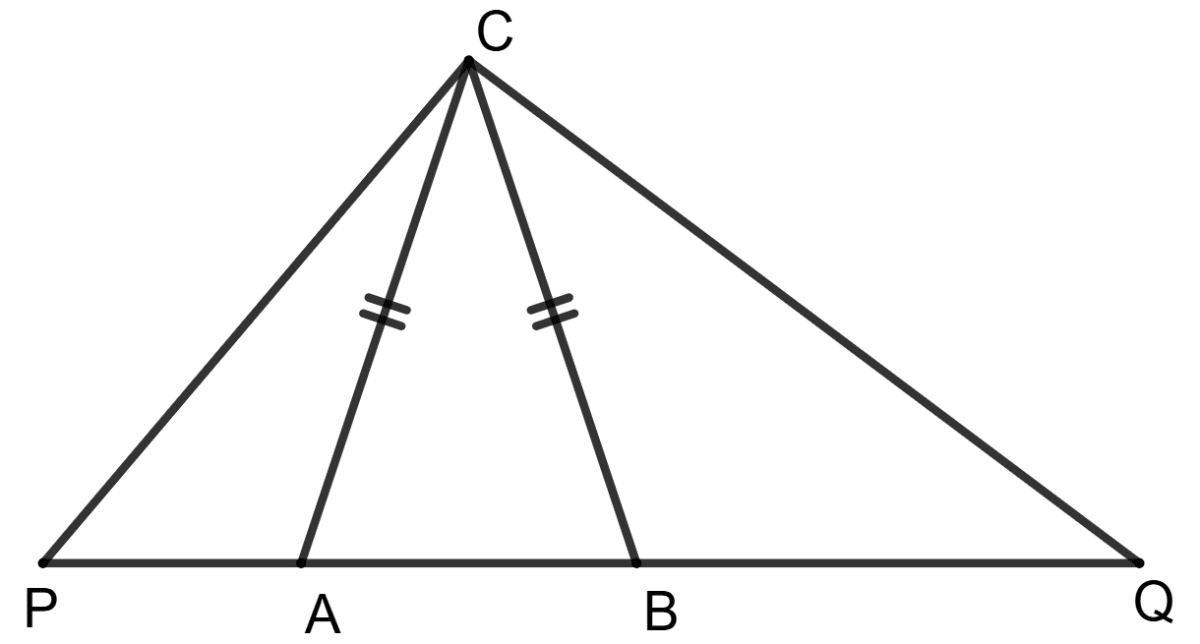
In the given figure, Δ ABC is isosceles and AP x BQ = AC2, prove that Δ ACP ∼ Δ BCQ.
If AE = 10 cm, BD = 8 cm and BC = 10 cm, then AB is equal to :
5 cm
25 cm
12.5 cm
2.5 cm
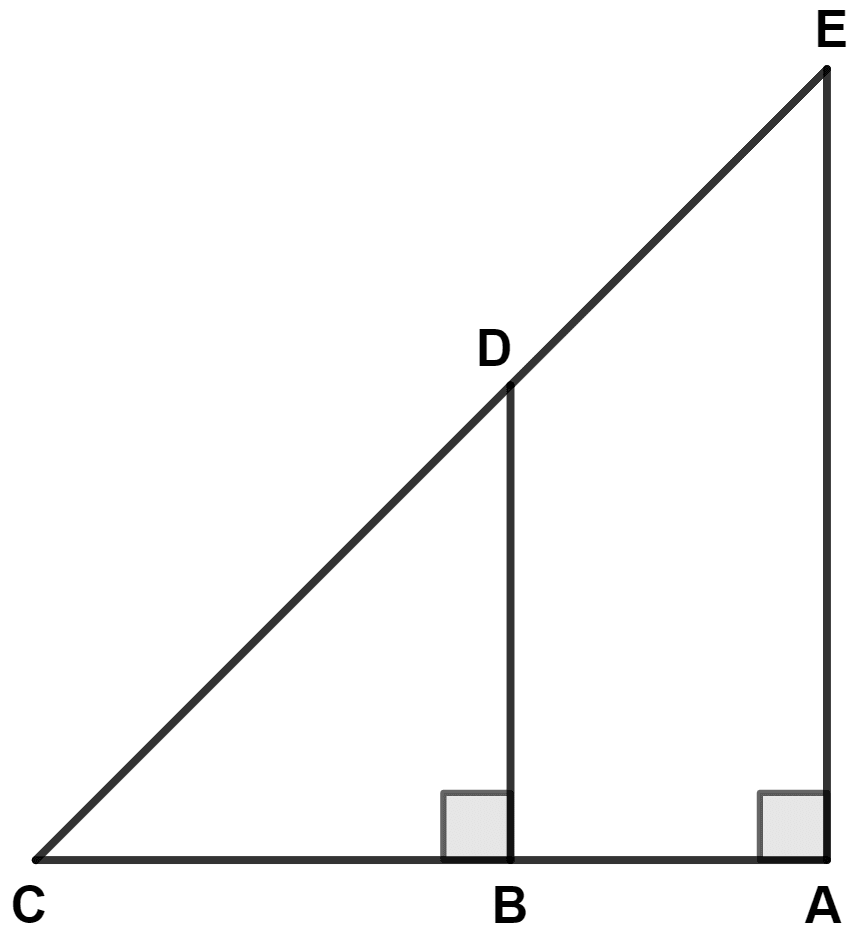
In the given figure :
△ ABE ~ △ ADE
△ ADE ~ △ ABC
△ ADE ~ △ BAC
△ ADE ~ △ CAB
