Mathematics
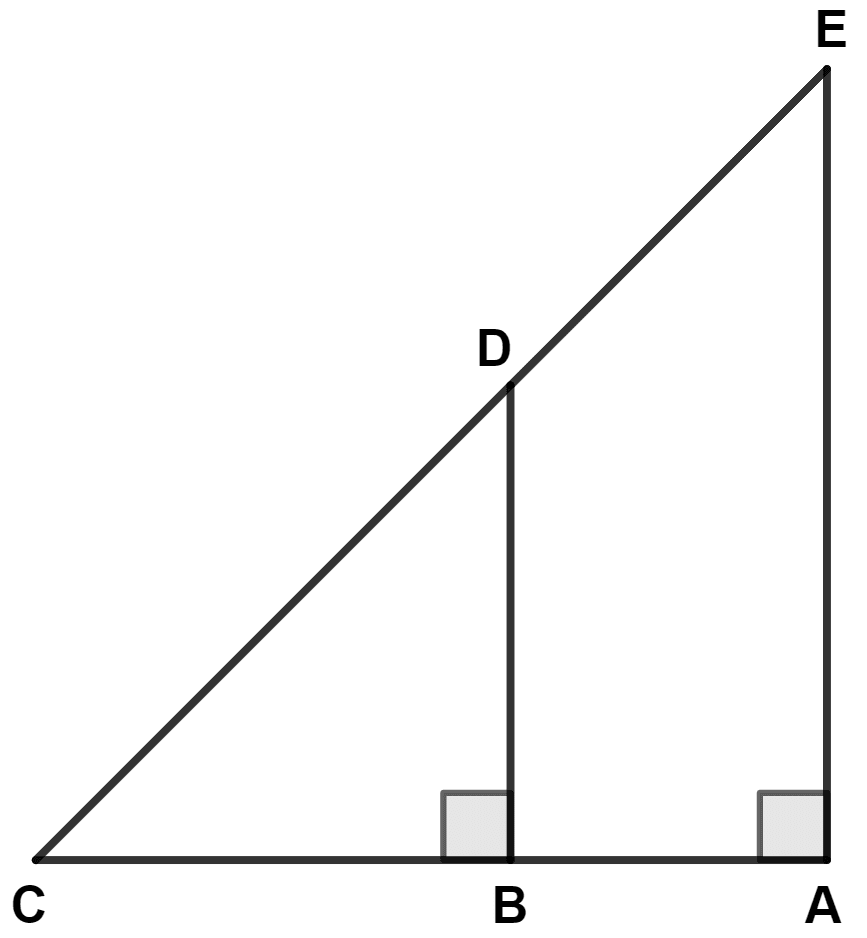
If AE = 10 cm, BD = 8 cm and BC = 10 cm, then AB is equal to :
5 cm
25 cm
12.5 cm
2.5 cm
Similarity
29 Likes
Answer
From figure,
In △ ACE and △ BCD,
⇒ ∠CAE = ∠CBD (Both equal to 90°)
⇒ ∠ACE = ∠BCD (Common angles)
Since, two angles of two triangles are equal so third angle of both the triangle will also be equal.
⇒ ∠CEA = ∠CDB.
∴ △ ACE ~ △ BCD (By A.A.A. postulate)
We know that,
Corresponding sides of similar triangle are in proportion.
From figure,
AB = AC - BC = 12.5 - 10 = 2.5 cm.
Hence, Option 4 is the correct option.
Answered By
18 Likes
Related Questions
In the given figure, Δ ABC is isosceles and AP x BQ = AC2, prove that Δ ACP ∼ Δ BCQ.
In triangle ABC, ∠BAC = 90° and AD is perpendicular to side BC. Triangle ABD is similar to triangle CBA by :
SAS
ASA
AAA
RHS
In the given figure :
△ ABE ~ △ ADE
△ ADE ~ △ ABC
△ ADE ~ △ BAC
△ ADE ~ △ CAB

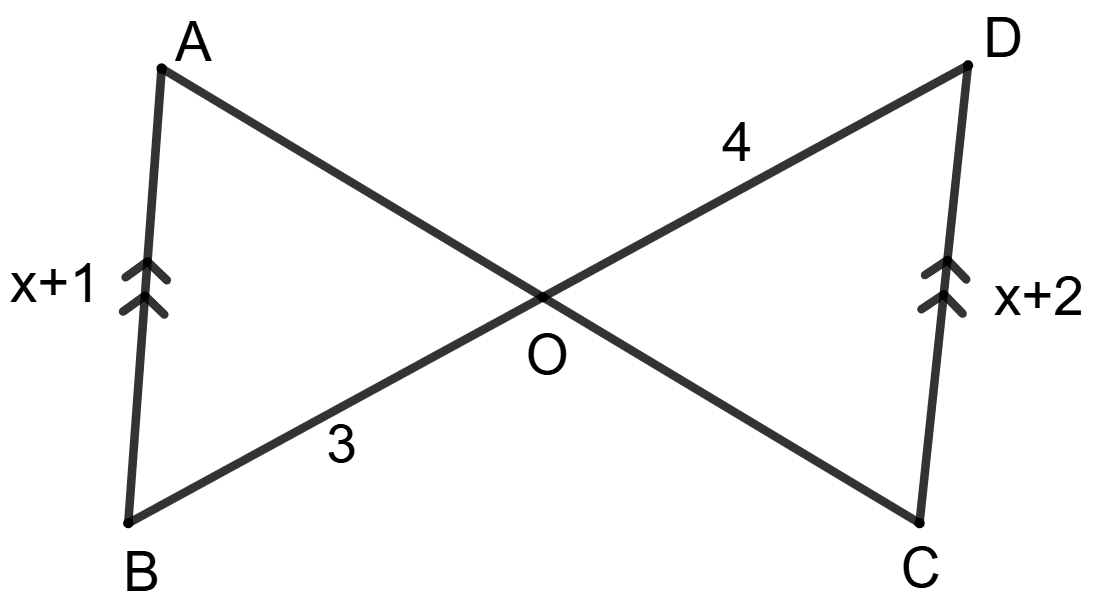
The value of x is :
2
3
1
none of these