Mathematics
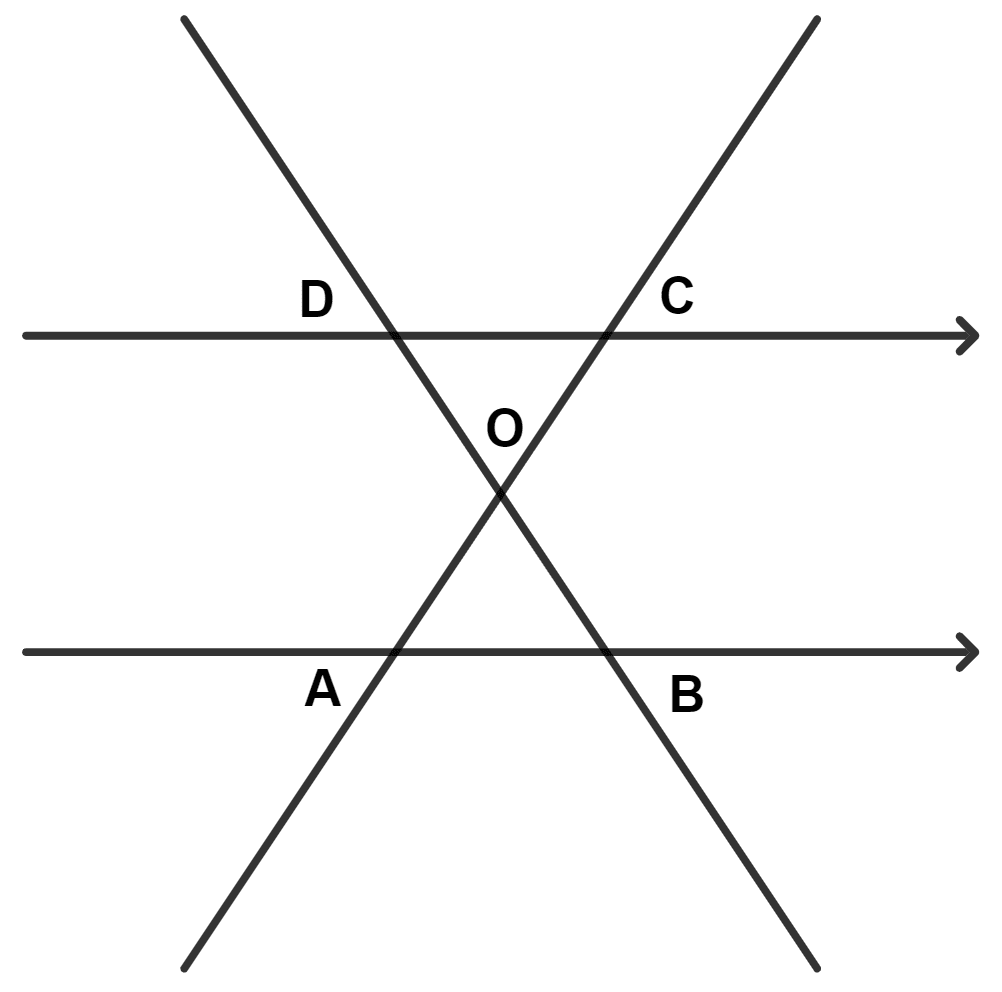
In the given diagram OC = 1.5 × OA, then OB is equal to :
3 × OD
1.5 × OD
× OD
OD
Similarity
13 Likes
Answer
From figure,
In △ OAB and △ OCD,
⇒ ∠AOB = ∠COD (Vertically opposite angles are equal)
⇒ ∠OAB = ∠OCD (Alternate angles are equal)
⇒ ∠OBA = ∠ODC (Alternate angles are equal)
∴ △ OAB ~ △ OCD (By A.A.A. postulate)
Given,
⇒ OC = 1.5 × OA
⇒ .
We know that,
Corresponding sides of similar triangle are in proportion.
Hence, Option 3 is the correct option.
Answered By
11 Likes
Related Questions
In triangle ABC, ∠BAC = 90° and AD is perpendicular to side BC. Triangle ABD is similar to triangle CBA by :
SAS
ASA
AAA
RHS
If AE = 10 cm, BD = 8 cm and BC = 10 cm, then AB is equal to :
5 cm
25 cm
12.5 cm
2.5 cm
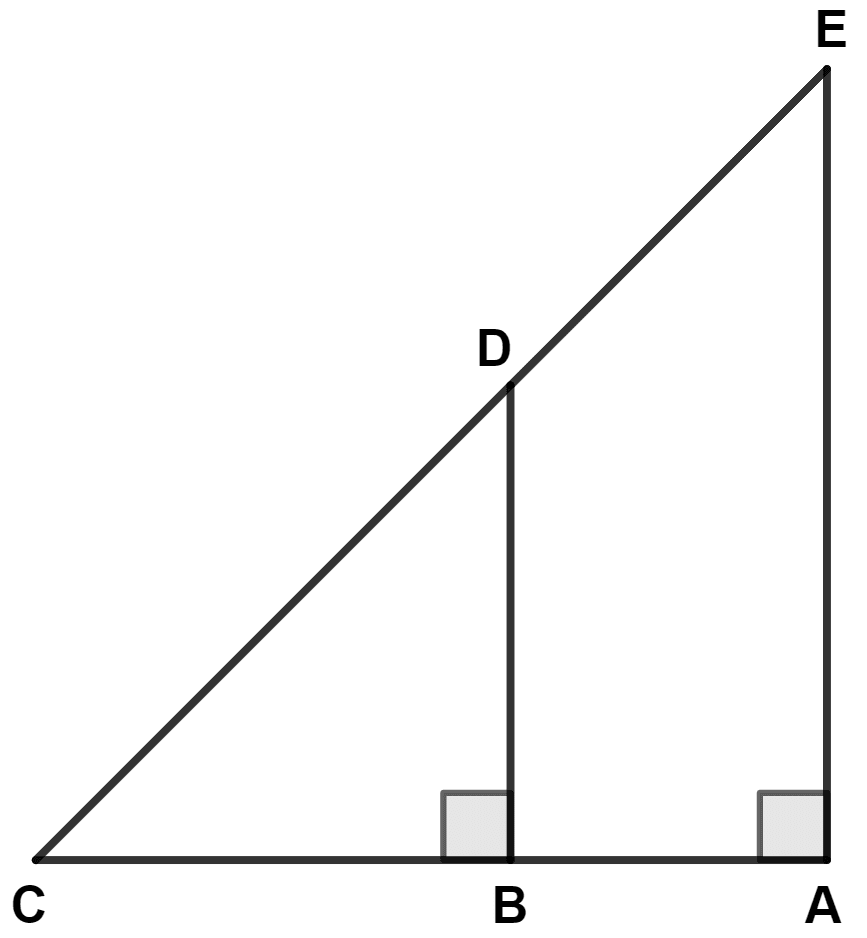
In the given figure :
△ ABE ~ △ ADE
△ ADE ~ △ ABC
△ ADE ~ △ BAC
△ ADE ~ △ CAB

In the given figure, OD = 2 × OB, OC = 2 × OA and CD = 2 × AB then △ AOB ~ △ COD by :
AA
SS
SAS
SSS
