Mathematics
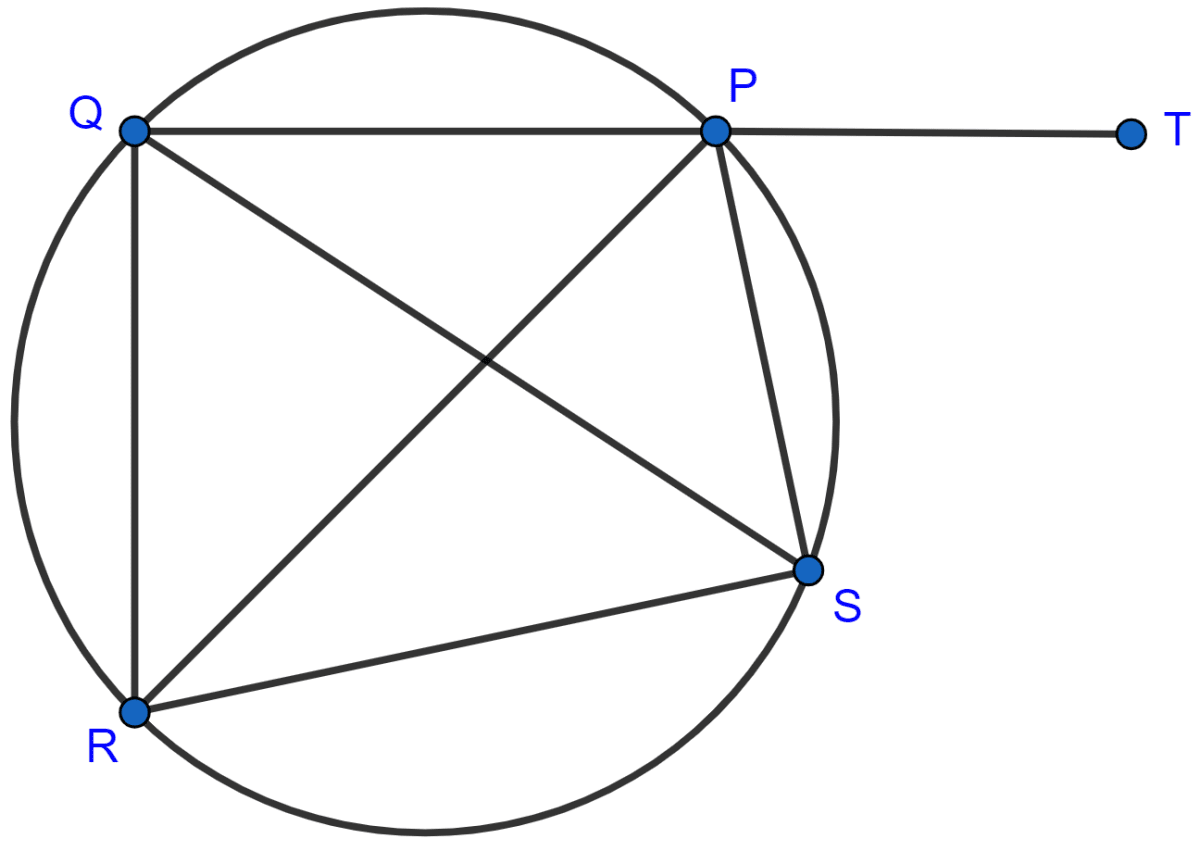
In the given figure, SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that :
SQ = SR.
Circles
21 Likes
Answer
PQRS is a cyclic quadrilateral.
Sum of opposite angles in a cyclic quadrilateral = 180°.
∴ ∠QRS + ∠QPS = 180° ………..(1)
Also,
∠QPS + ∠SPT = 180° [As QPT is a straight line] ……..(2)
Subtracting equation (2) from (1) we get,
⇒ ∠QRS + ∠QPS - (∠QPS + ∠SPT) = 180° - 180°
⇒ ∠QRS - ∠SPT = 0
⇒ ∠QRS = ∠SPT ……….(3)
∠RQS = ∠RPS [Angles in same segment are equal] ……..(4)
∠RPS = ∠SPT [As PS bisects ∠RPT] …….(5)
From (3), (4) and (5) we get :
⇒ ∠QRS = ∠RQS.
∴ SQ = SR [As sides opposite to equal angles are also equal]
Hence, proved that SQ = SR.
Answered By
14 Likes
Related Questions
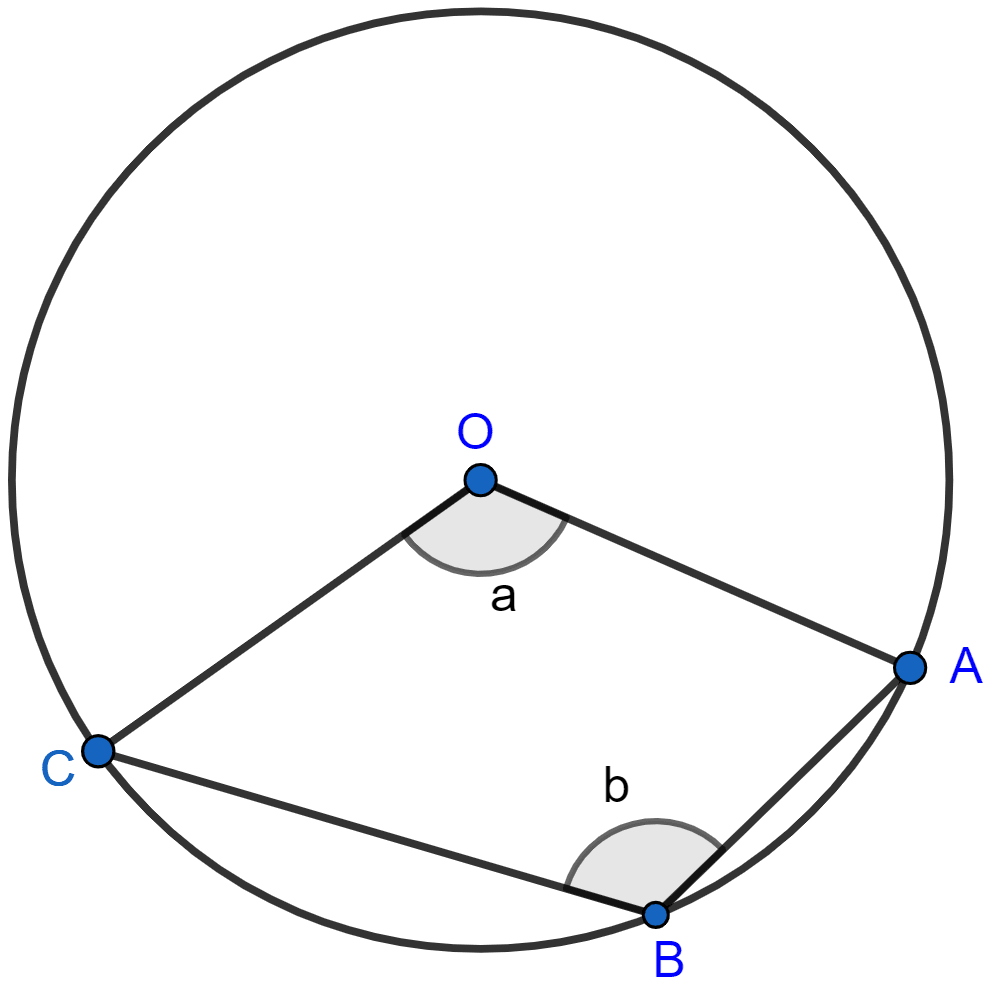
The figure given below, shows a circle with centre O.
Given : ∠AOC = a and ∠ABC = b.
(i) Find the relationship between a and b.
(ii) Find the measure of angle OAB, if OABC is a parallelogram.
In the figure given, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°.
Calculate :
(i) ∠RNM,
(ii) ∠NRM.

In the figure, O is the center of the circle, ∠AOE = 150°, ∠DAO = 51°. Calculate the sizes of the angles CEB and OCE.
In the figure, given below, P and Q are the centers of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x.
