Mathematics
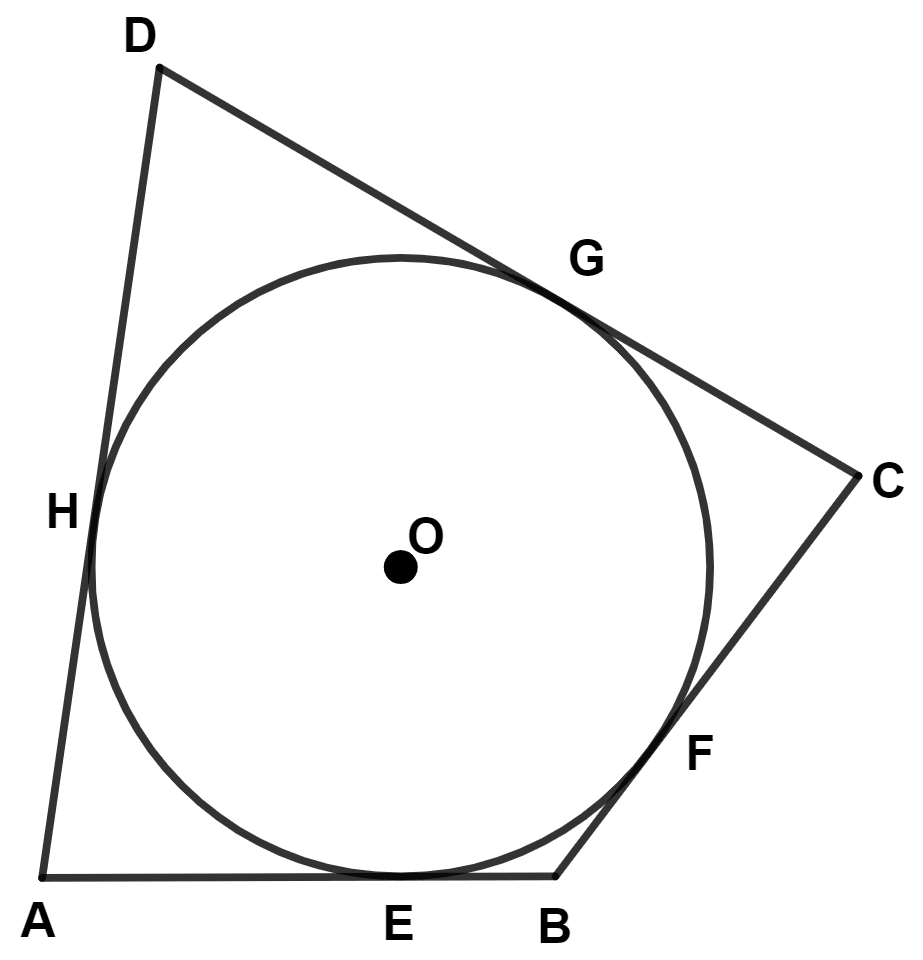
In the given figure O is the centre of the circle. ABCD is a quadrilateral where sides AB, BC, CD and DA touch the circle at E, F, G and H respectively. If AB = 15 cm, BC = 18 cm and AD = 24 cm, find the length of CD.
Answer
We know that,
The length of tangents drawn from an external point to the circle are equal.
⇒ AE = AH = x (let)
⇒ BE = BF = y (let)
⇒ CF = CG = z (let)
⇒ DG = DH = k (let)
Given,
⇒ AB = 15
⇒ AE + EB = 15
⇒ x + y = 15 …….(1)
⇒ BC = 18
⇒ BF + CF = 18
⇒ y + z = 18 ……..(2)
⇒ AD = 24
⇒ AH + DH = 24
⇒ x + k = 24 ……….(3)
Adding equations (2) and (3), we get :
⇒ y + z + x + k = 18 + 24
⇒ x + y + z + k = 42
⇒ 15 + z + k = 42 [From equation (1)]
⇒ z + k = 42 - 15
⇒ z + k = 27.
⇒ CD = CG + DG = k + z = 27 cm.
Hence, length of CD = 27 cm.
Related Questions
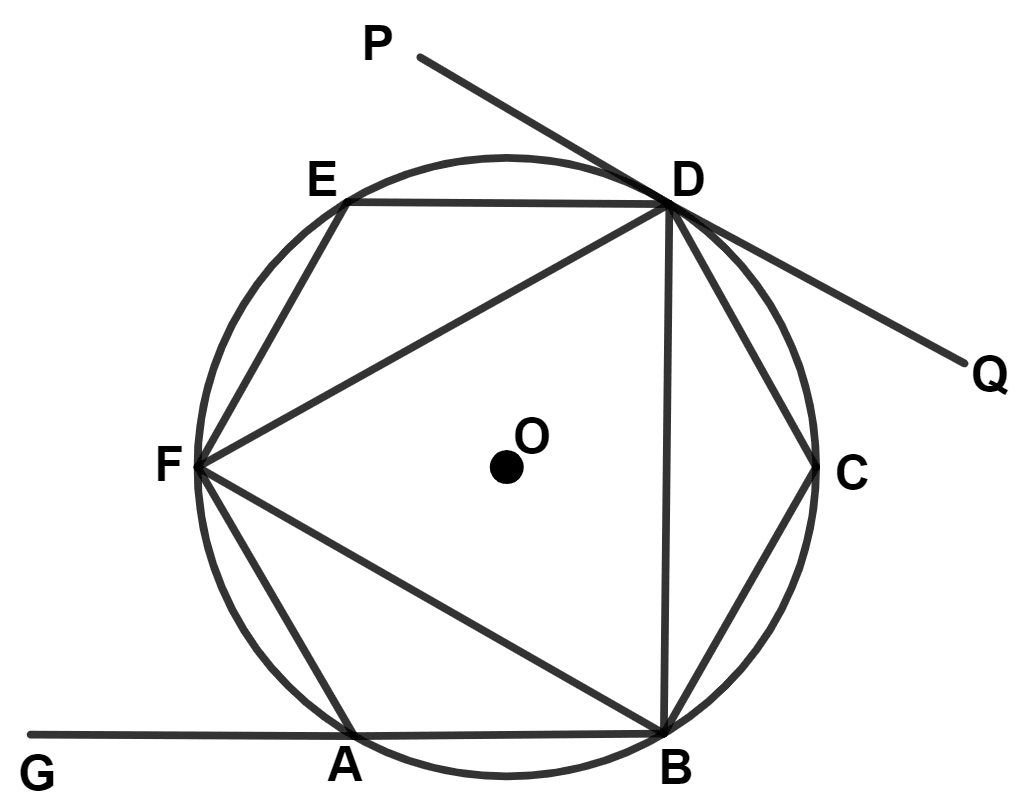
In the given diagram, ABCDEF is a regular hexagon inscribed in a circle with centre O. PQ is a tangent to the circle at D. Find the value of :
(a) ∠FAG
(b) ∠BCD
(c) ∠PDE
Construct a triangle ABC such that AB = 7 cm, BC = 6 cm and CA = 5 cm.
(a) Draw the locus of the points such that
(i) it is equidistant from BC and BA.
(ii) it is equidistant from points A and B.
(b) Mark P where the loci (i) and (ii) meet, measure and write length of PA.
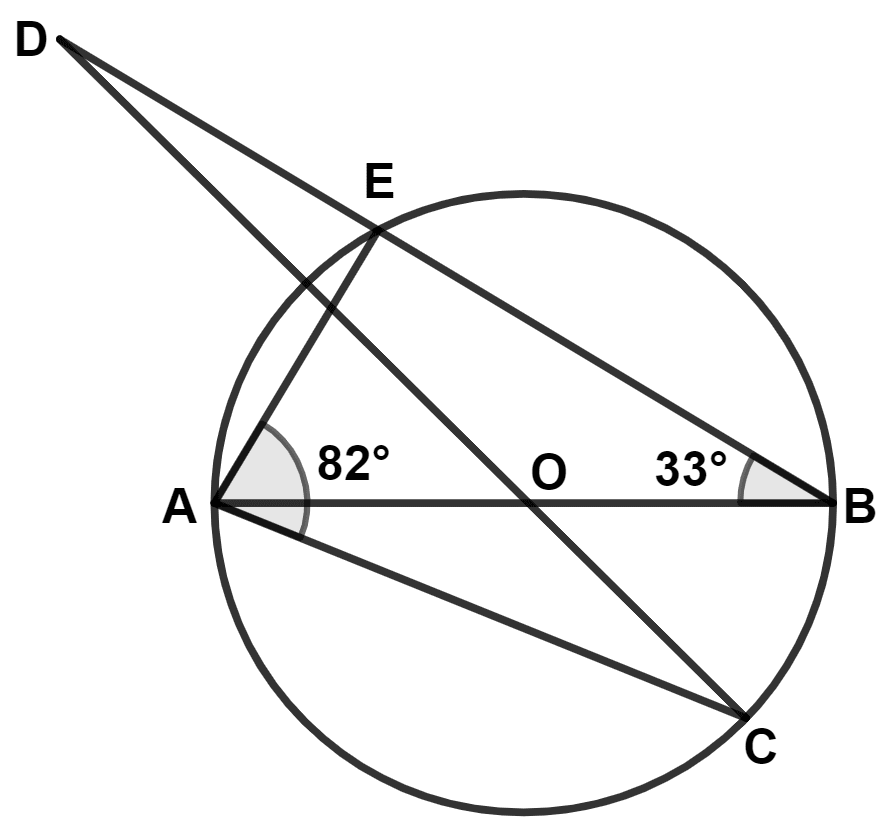
AB and CD intersect at the center O of the circle given in the above diagram. If ∠EBA = 33° and ∠EAC = 82°, find
(a) ∠BAE
(b) ∠BOC
(c) ∠ODB
In the extract of Survey of India map G43S7, prepared on a scale of 2 cm to 1 km, a child finds the length of the cart track between two settlements is 7.6 cm. Find :
(a) the actual length of the cart track on the ground.
(b) actual area of a grid square, if each has an area of 4 cm2.