Mathematics
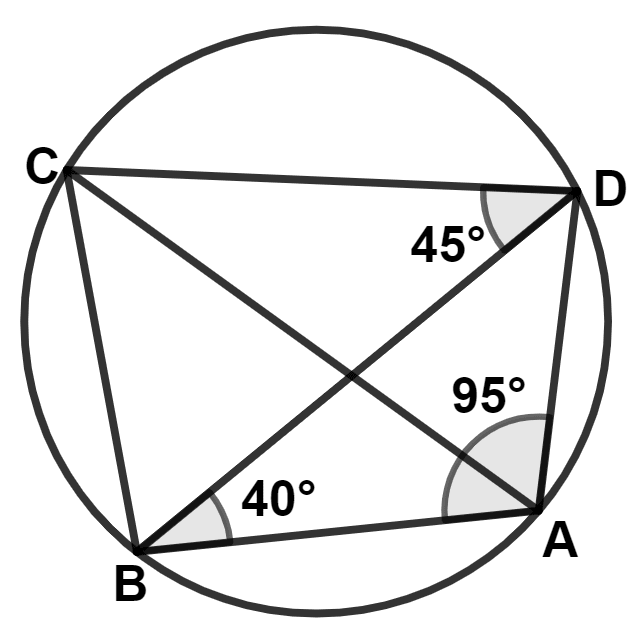
In the given figure, O is center of the circle and OABC is a rhombus, then :
x° + y° = 180°
x° = y° = 90°
x° + 2y° = 360°
x° = y° = 45°

Related Questions
In the given figure x°, y°, z° and p° are exterior angles of cyclic quadrilateral ABCD, then x° + y° + z° + p° is :
180°
270°
360°
720°

Arcs AB and BC are of lengths in the ratio 11 : 4 and O is center of the circle. If angle BOC = 32°, the angle AOB is :
64°
88°
128°
132°

In the given figure, AB is the side of regular pentagon and BC is the side of regular hexagon. Angle BAC is :
132°
66°
90°
120°
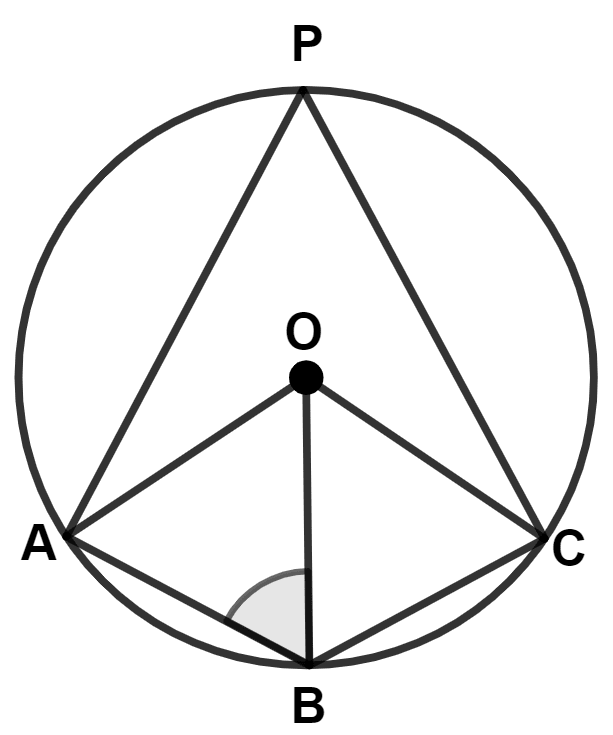
In the given circle, ∠BAD = 95°, ∠ABD = 40° and ∠BDC = 45°.
Assertion (A) : To show that AC is a diameter, the angle ADC or angle ABC need to be proved to be 90°.
Reason (R) : In △ADB,
∠ADB = 180° - 95° - 40° = 45°
∴ Angle ADC = 45° + 45° = 90°
(i) A is true, R is false
(ii) A is true, R is true
(iii) A is false, R is false
(iv) A is false, R is true