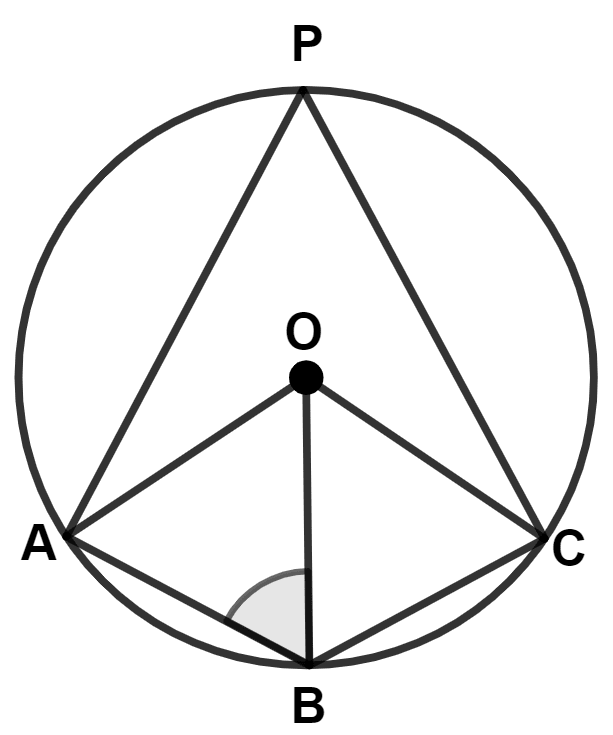
Mathematics
In the given figure, O is center of the circle and OABC is a rhombus, then :
x° + y° = 180°
x° = y° = 90°
x° + 2y° = 360°
x° = y° = 45°

Circles
Answer
Join OB.
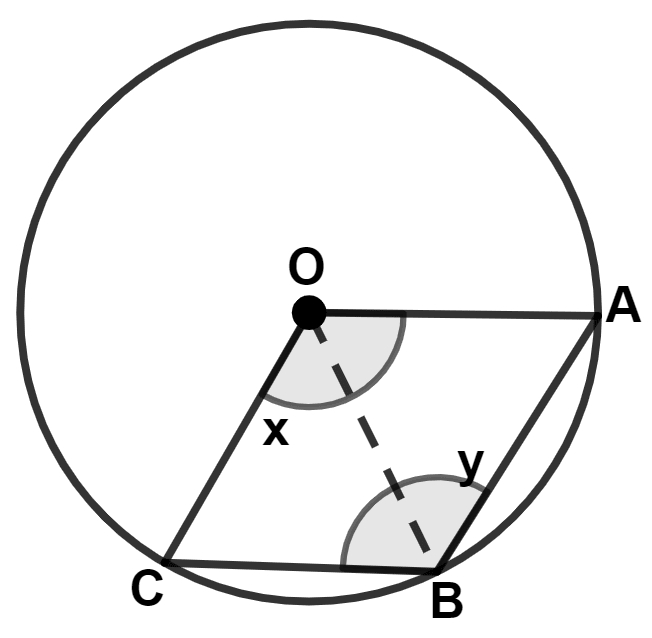
From figure,
OB = OA (Radius of same circle) ……..(1)
We know that,
Sides of rhombus are equal.
∴ OA = AB ………….(2)
From (1) and (2), we get :
⇒ OA = OB = AB
∴ OAB is an equilateral triangle.
Since, diagonals of rhombus bisect the interior angles.
In △OAB,
∠AOB =
∠OBA =
Since, each angle of equilateral triangle is 60°.
∴ ∠AOB = 60°
⇒
⇒ x = 120°.
∴ ∠OBA = 60°
⇒
⇒ y = 120°.
Substituting value of x and y in L.H.S. of equation x° + 2y° = 360°, we get :
⇒ 120° + 2(120°)
⇒ 120° + 240°
⇒ 360°.
Since, L.H.S. = R.H.S.
Hence, Option 3 is the correct option.
Answered By
Related Questions
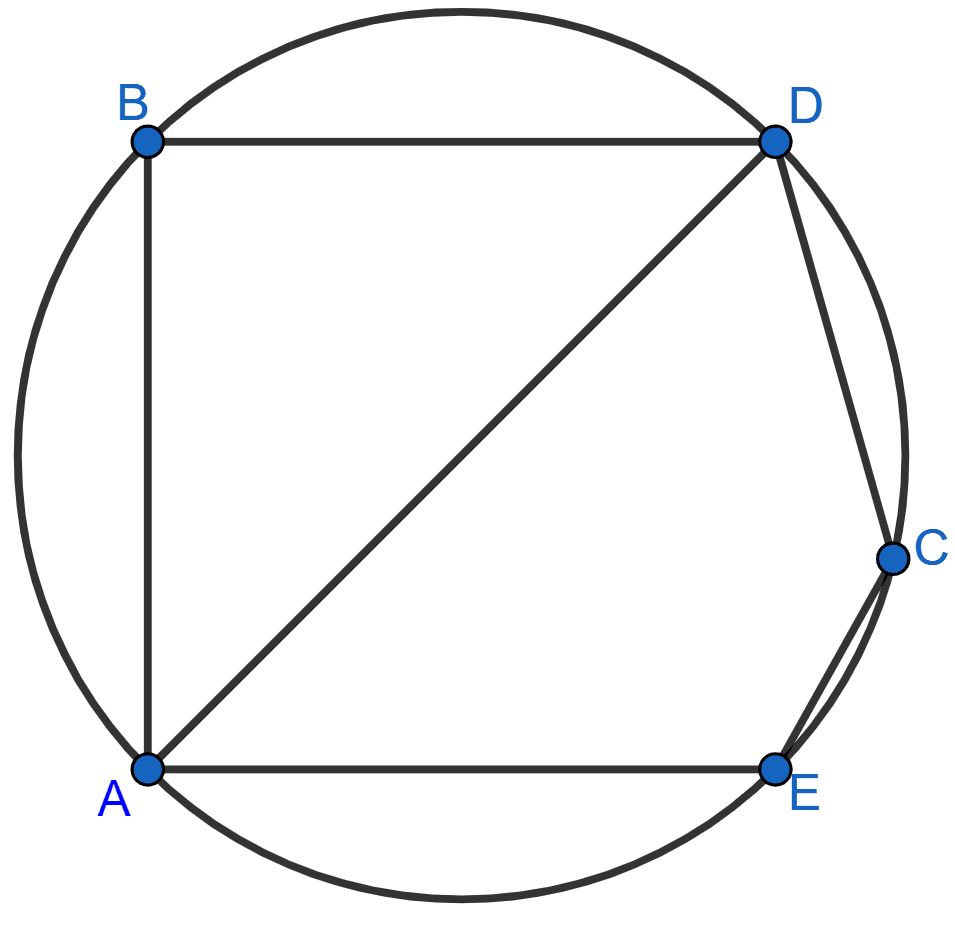
In the given figure, BD is a side of regular hexagon, DC is a side of a regular pentagon and AD is a diameter. Calculate :
(i) ∠ADC,
(ii) ∠BDA,
(iii) ∠ABC,
(iv) ∠AEC.
In the given figure x°, y°, z° and p° are exterior angles of cyclic quadrilateral ABCD, then x° + y° + z° + p° is :
180°
270°
360°
720°

Arcs AB and BC are of lengths in the ratio 11 : 4 and O is center of the circle. If angle BOC = 32°, the angle AOB is :
64°
88°
128°
132°

In the given figure, AB is the side of regular pentagon and BC is the side of regular hexagon. Angle BAC is :
132°
66°
90°
120°