Mathematics
In the given figure, . Find AB if DC = 24 cm.
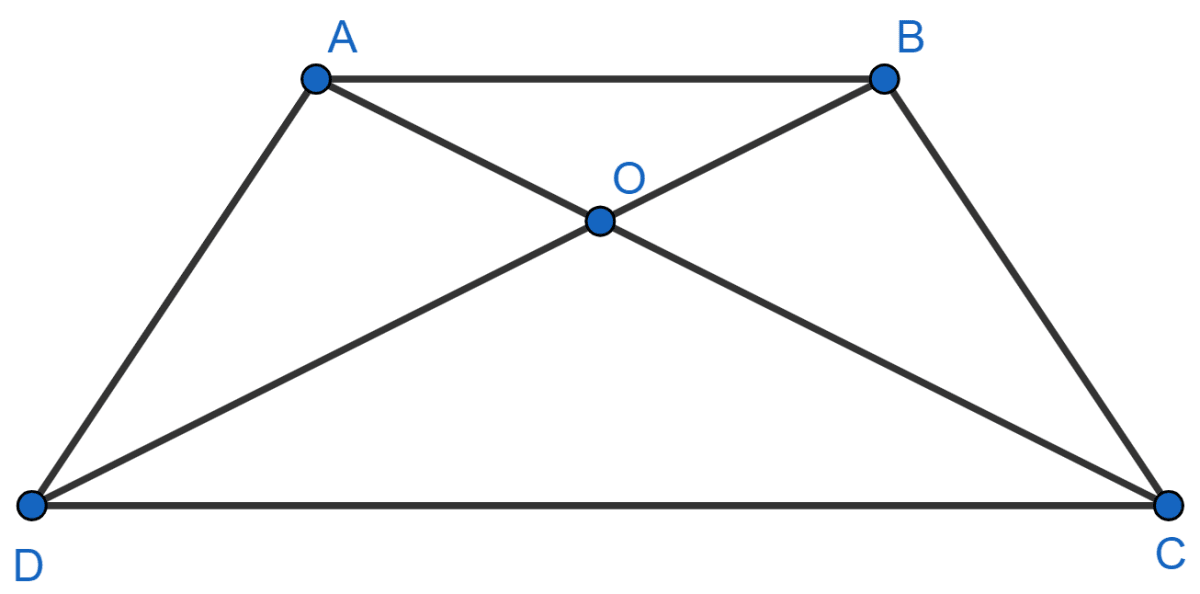
Similarity
1 Like
Answer
Since,
(Given)
∠AOB = ∠COD (Vertically opposite angles are equal).
∴ △AOB ~ △COD
Since, ratio of corresponding sides of similar triangles are proportional.
Hence, AB = 9.6 cm
Answered By
3 Likes
Related Questions
Using assumed mean method, calculate the mean.
Class-interval Frequency 0-30 22 30-60 30 60-90 40 90-120 36 120-150 28 150-180 20 Find the set of values of x satisfying 7x + 3 ≥ 3x - 5 and ∈ N.
If two pipes function simultaneously, the reservoir will be filled in 12 hours. One pipe fills the empty reservoir 10 hours faster than the other. How many hours does it take the second pipe to fill the reservoir ?
The marks of 200 students are as given below :
Marks No. of students 20-29 7 30-39 11 40-49 20 50-59 46 60-69 57 70-79 37 80-89 15 90-99 7 Draw a cumulative frequency curve and find :
(i) median marks
(ii) if 80% of the students passed, find the passing marks.