Mathematics
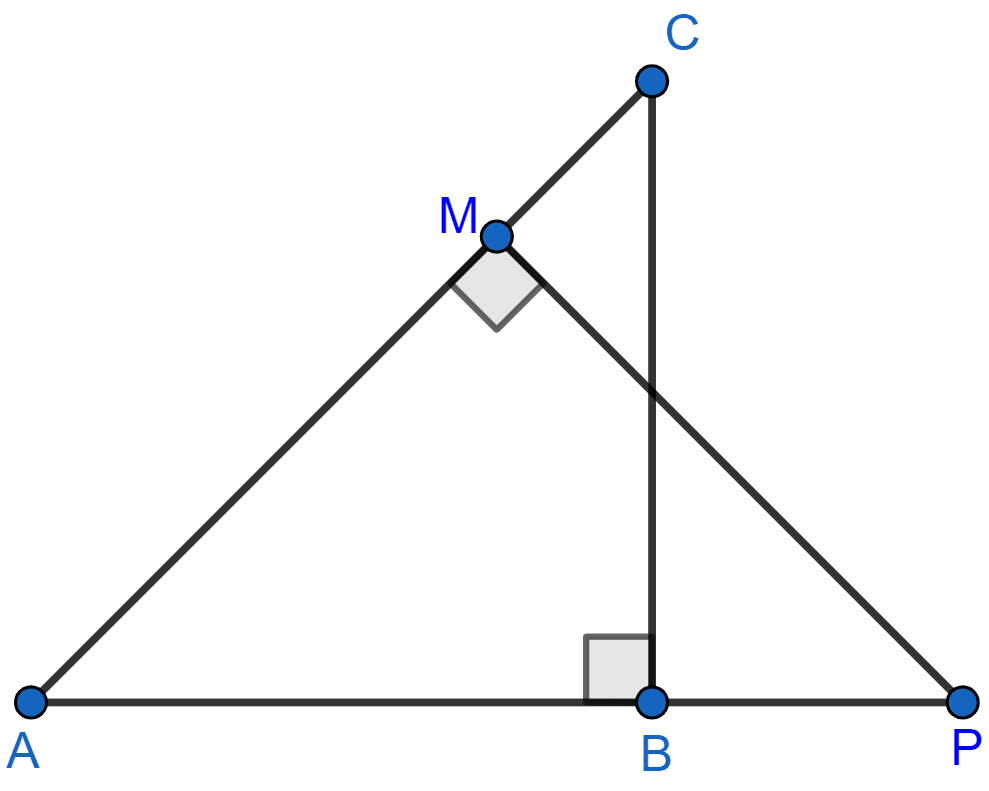
In the given figure, ΔABC and ΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove that : ∆ABC ~ ∆AMP.
(ii) Find AB and BC.
Similarity
8 Likes
Answer
(i) In ∆ABC and ∆AMP, we have
⇒ ∠BAC = ∠PAM [Common]
⇒ ∠ABC = ∠PMA [Each = 90°]
∴ ∆ABC ~ ∆AMP [By AA]
Hence, proved that, ∆ABC ~ ∆AMP.
(ii) In right angle triangle AMP,
By pythagoras theorem,
⇒ AP2 = AM2 + MP2
⇒ AM2 = AP2 - MP2
⇒ AM2 = 152 - 122
⇒ AM2 = 225 - 144
⇒ AM2 = 81
⇒ AM = = 9 cm.
Since, corresponding sides of similar triangles are proportional we have :
Also,
Hence, AB = 6 cm and BC = 8 cm.
Answered By
5 Likes
Related Questions
In △ABC, ∠B = 90° and BD ⊥ AC.
(i) If CD = 10 cm and BD = 8 cm; find AD.
(ii) If AC = 18 cm and AD = 6 cm; find BD.
(iii) If AC = 9 cm and AB = 7 cm; find AD.
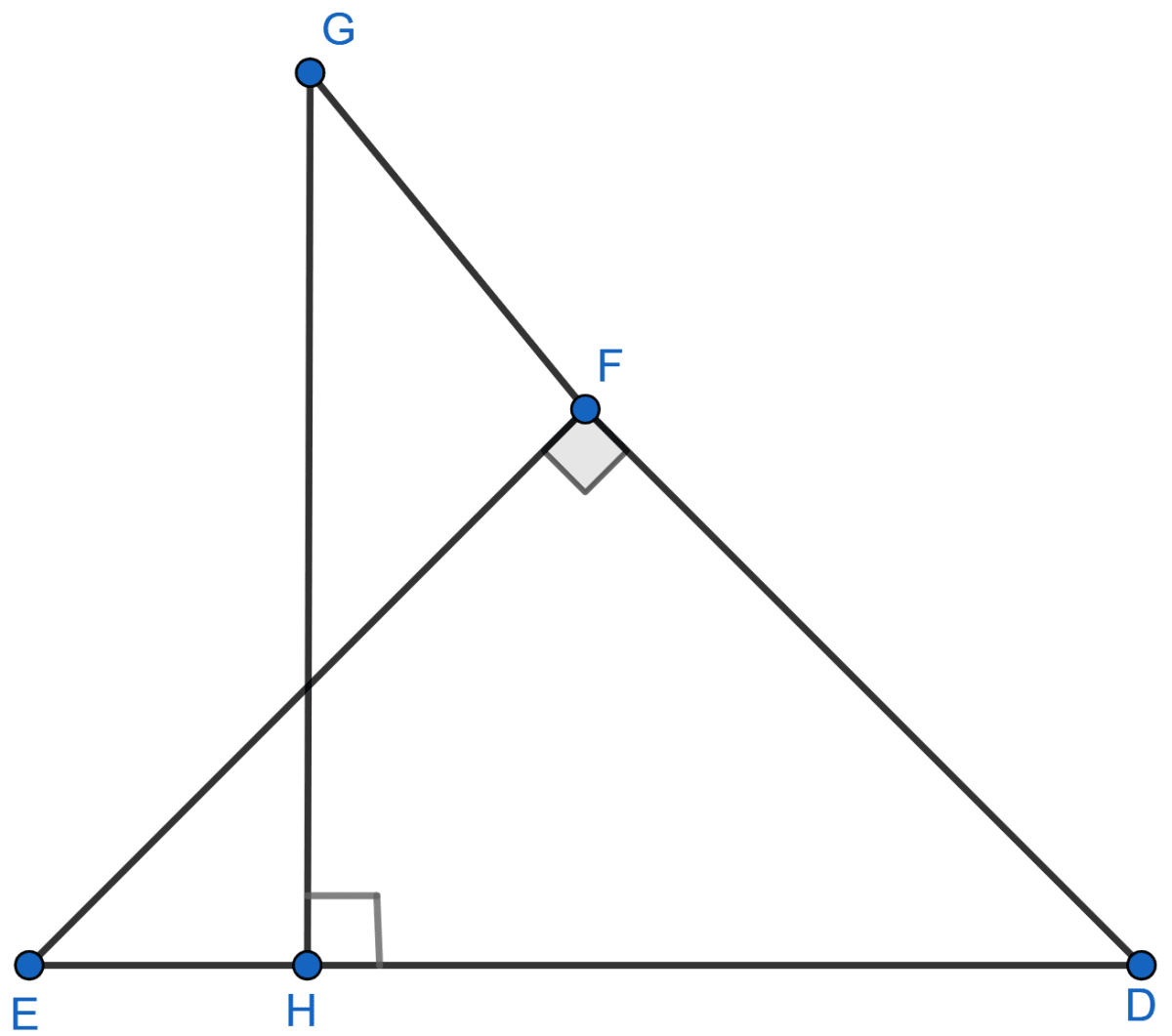
Given: ∠GHE = ∠DFE = 90°, DH = 8, DF = 12, DG = 3x – 1 and DE = 4x + 2.
Find: the lengths of segments DG and DE.
In △PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that :
(i) PQ2 = PM × PR
(ii) QR2 = PR × MR
(iii) PQ2 + QR2 = PR2
D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that: CA2 = CB x CD.