Mathematics
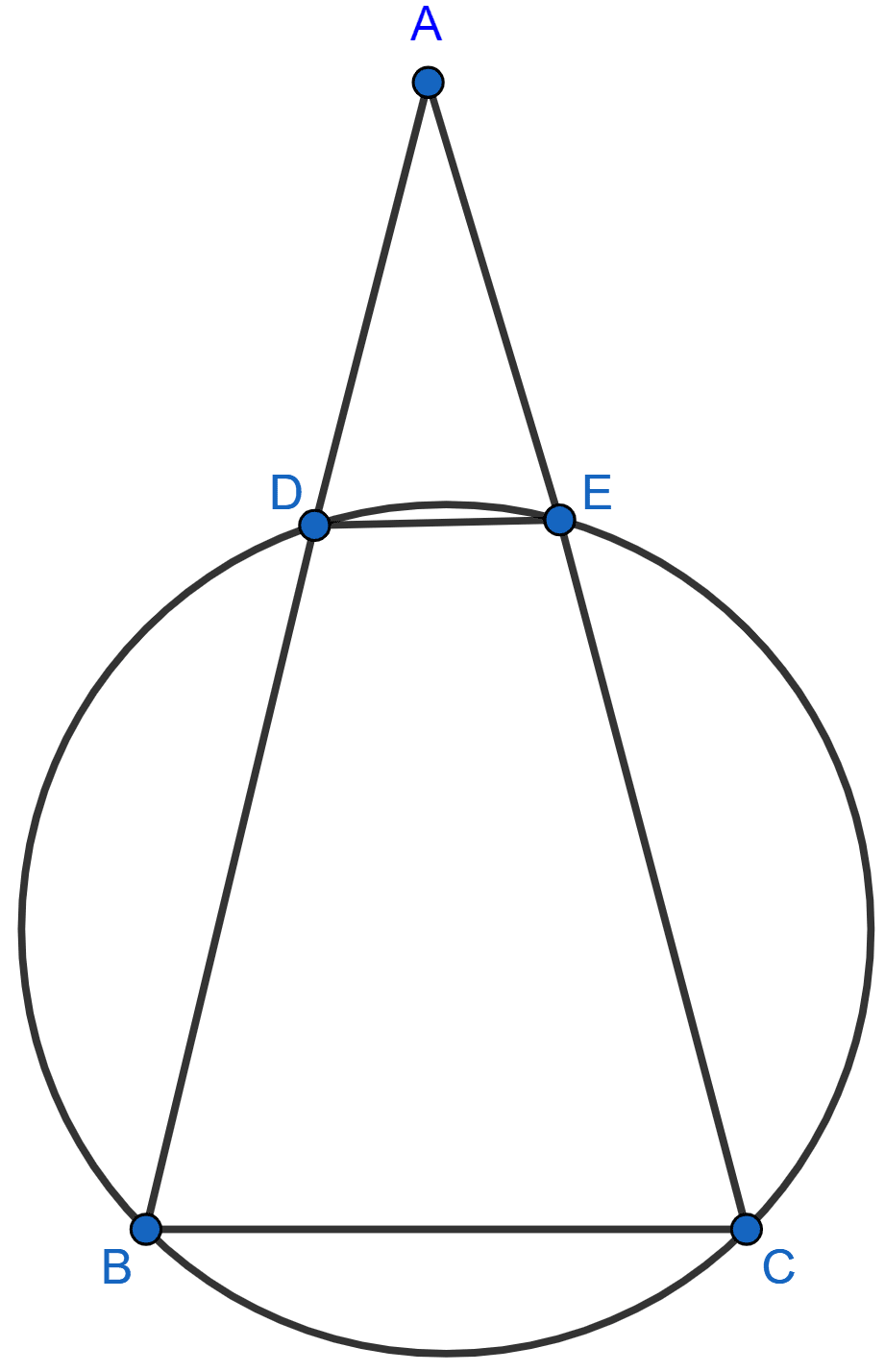
In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
Circles
7 Likes
Answer
Given, AB = AC
So, ∠B = ∠C ……..(1) [As Angles opposite to equal sides are equal]
From figure,
DECB is a cyclic quadrilateral.
∴ ∠B + ∠DEC = 180° [Sum of opposite angles in cyclic quadrilateral = 180°]
⇒ ∠C + ∠DEC = 180° (Using 1)
But this is the sum of interior angles on one side of a transversal.
∴ DE || BC.
∴ ∠ADE = ∠B and ∠AED = ∠C [Corresponding angles]
Thus, ∠ADE = ∠AED
∴ AD = AE
⇒ AB - AD = AC - AE [As AB = AC]
⇒ BD = CE
Hence, we have DE || BC and BD = CE.
Hence, proved that DECB is an isosceles trapezium.
Answered By
5 Likes
Related Questions
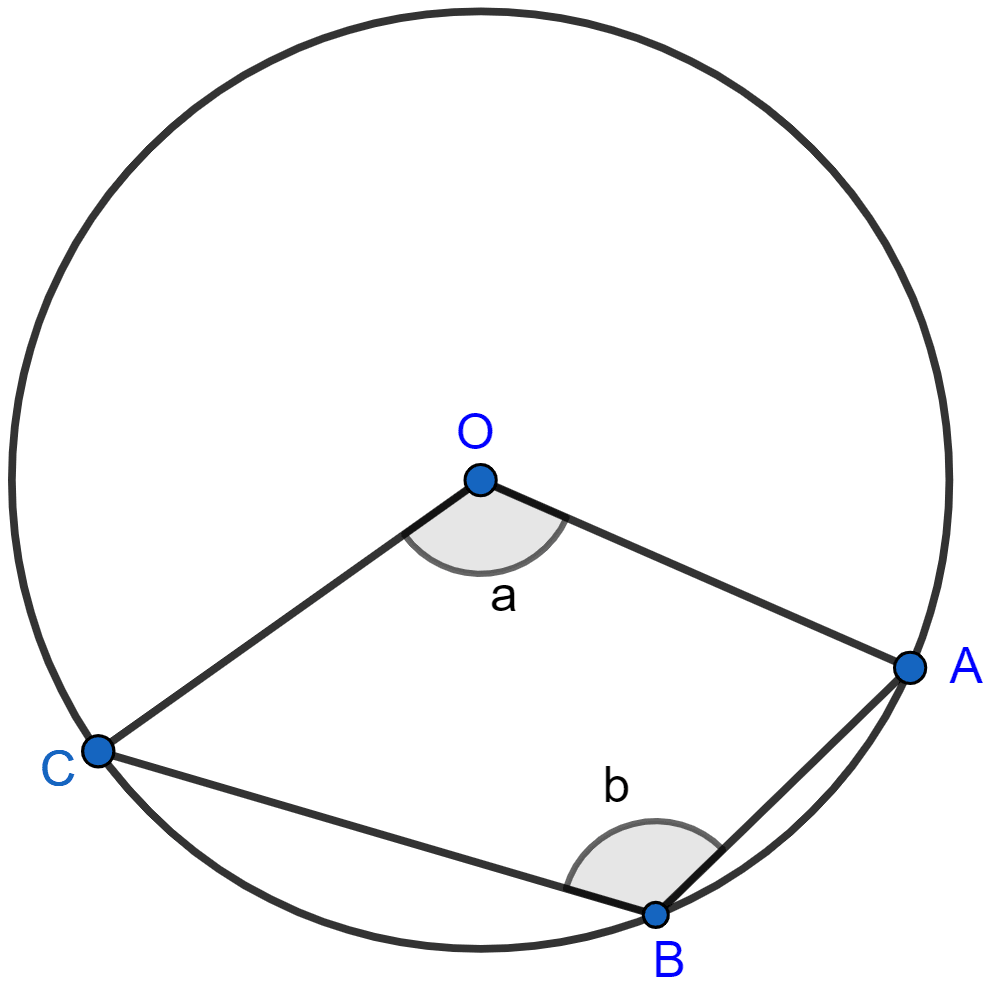
The figure given below, shows a circle with centre O.
Given : ∠AOC = a and ∠ABC = b.
(i) Find the relationship between a and b.
(ii) Find the measure of angle OAB, if OABC is a parallelogram.
Prove that:
(i) the parallelogram, inscribed in a circle, is a rectangle.
(ii) the rhombus, inscribed in a circle, is a square.
In the figure given, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°.
Calculate :
(i) ∠RNM,
(ii) ∠NRM.
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.