Mathematics
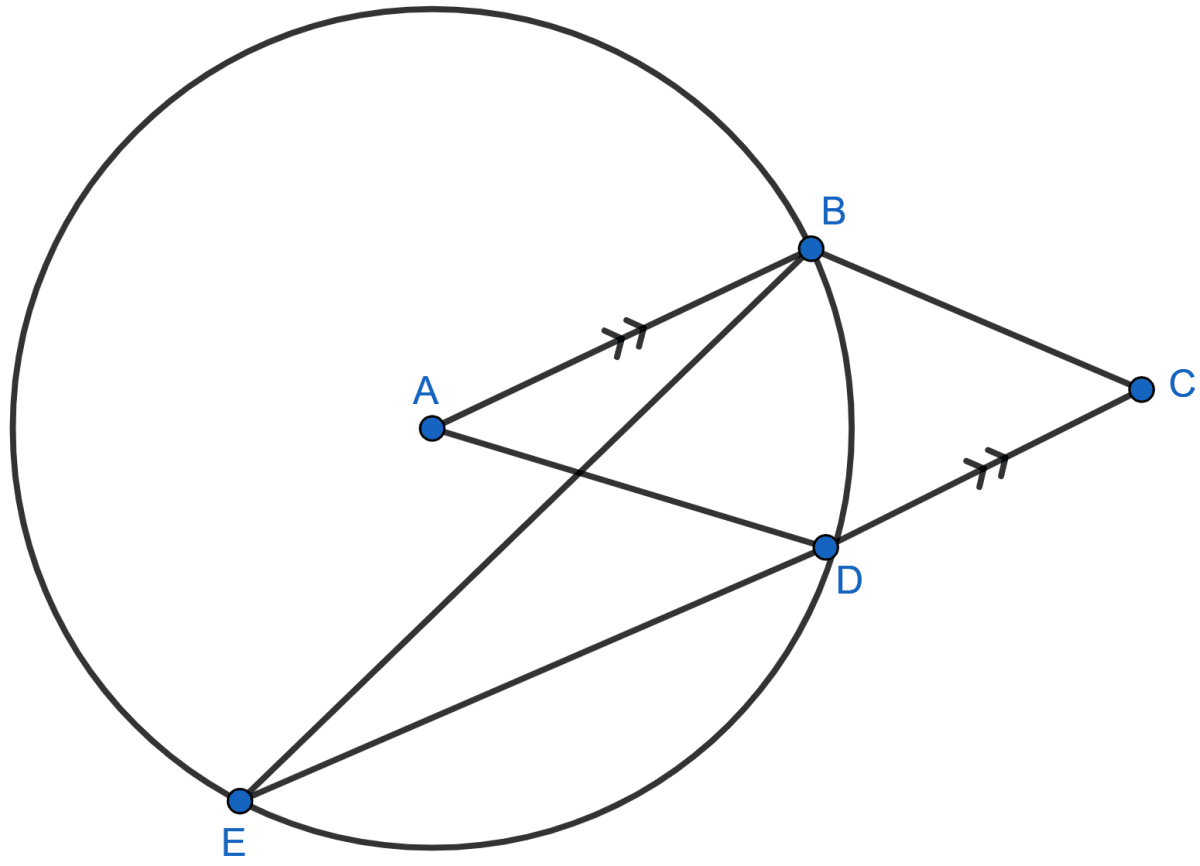
In the given figure, A is the center of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that : ∠BCD = 2∠ABE.
Answer
∠BAD = 2∠BED [Angle at the center is double the angle at the circumference subtended by the same chord.]
Since, CDE is a straight line and CD || AB.
∴ AB || ED.
⇒ ∠BED = ∠ABE [Alternate angles are equal]
Multiplying above equation by 2 we get,
⇒ 2∠BED = 2∠ABE
⇒ ∠BAD = 2∠ABE ……………(1)
ABCD is a parallelogram.
⇒ ∠BAD = ∠BCD [Opposite angles of a paralellogram are equal] ……….(2)
From (1) and (2) we get,
⇒ ∠BCD = 2∠ABE.
Hence, proved that ∠BCD = 2∠ABE.
Related Questions
In the given figure, AB = AC = CD and ∠ADC = 38°. Calculate :
(i) Angle ABC
(ii) Angle BEC

In the given figure, I is the incenter of △ABC, BI when produced meets the circumcircle of △ABC at D. Given, ∠BAC = 55° and ∠ACB = 65°; calculate :
(i) ∠DCA,
(ii) ∠DAC,
(iii) ∠DCI,
(iv) ∠AIC.
In the figure given alongside, AB || CD and O is the center of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find :
(i) ∠PRB,
(ii) ∠PBR,
(iii) ∠BPR.