Mathematics
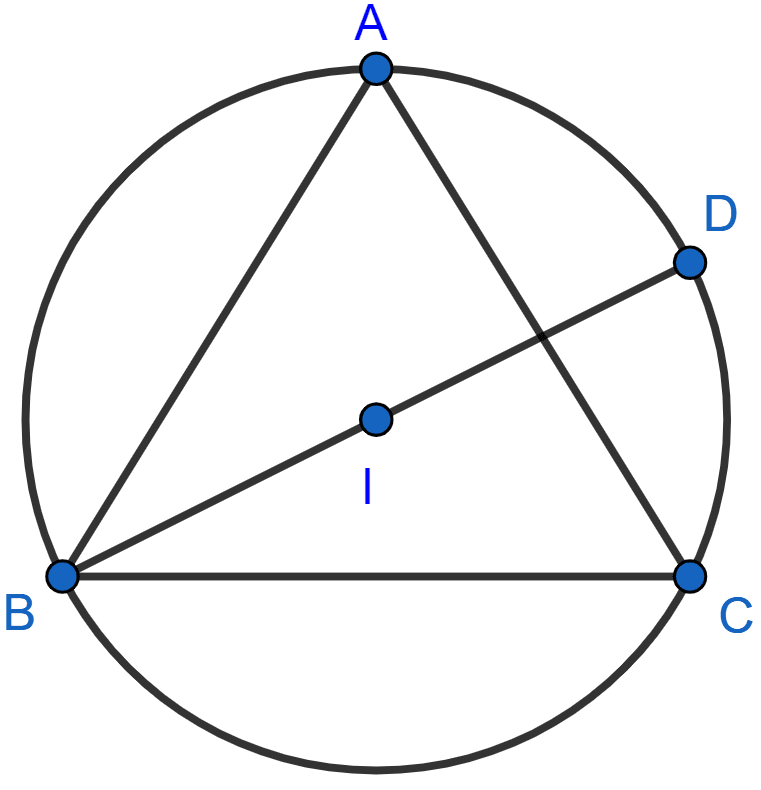
In the given figure, I is the incenter of △ABC, BI when produced meets the circumcircle of △ABC at D. Given, ∠BAC = 55° and ∠ACB = 65°; calculate :
(i) ∠DCA,
(ii) ∠DAC,
(iii) ∠DCI,
(iv) ∠AIC.
Circles
20 Likes
Answer
(i) Join IA, IC and CD.
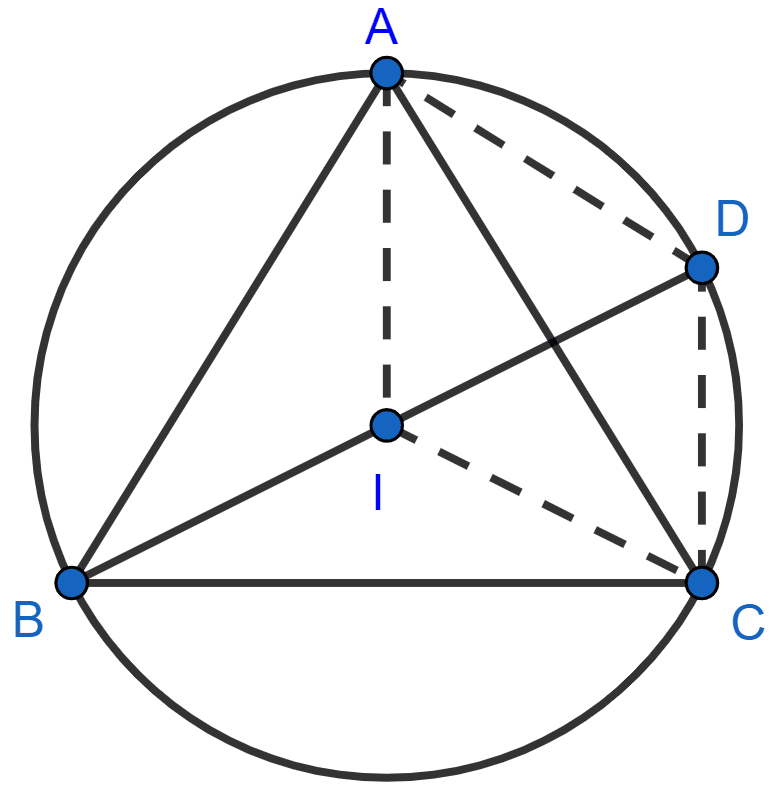
In △ABC,
⇒ ∠ABC + ∠BAC + ∠ACB = 180°
⇒ ∠ABC + 55° + 65° = 180°
⇒ ∠ABC + 120° = 180°
⇒ ∠ABC = 180° - 120° = 60°.
IB is the bisector of ∠ABC [As I is the incenter].
∠ABD = ∠ABC = x 60° = 30°.
We know that,
Angle in same segment are equal.
∴ ∠DCA = ∠ABD = 30°.
Hence, ∠DCA = 30°.
(ii) ∠CBD = ∠ABD = 30° [As IB is bisector of ∠ABC]
We know that,
Angle in same segment are equal.
∴ ∠DAC = ∠CBD = 30°.
Hence, ∠DAC = 30°.
(iii) As CI is the angle bisector of ∠ACB.
∠ACI = ∠ACB = = 32.5°
From figure,
∠DCI = ∠DCA + ∠ACI = 30° + 32.5° = 62.5°
Hence, ∠DCI = 62.5°.
(iv) As AI is the angle bisector of ∠BAC.
∠IAC = ∠BAC = = 27.5°
In △AIC,
⇒ ∠IAC + ∠ACI + ∠AIC = 180°
⇒ 27.5° + 32.5° + ∠AIC = 180°
⇒ 60° + ∠AIC = 180°
⇒ ∠AIC = 180° - 60° = 120°.
Hence, ∠AIC = 120°.
Answered By
11 Likes
Related Questions
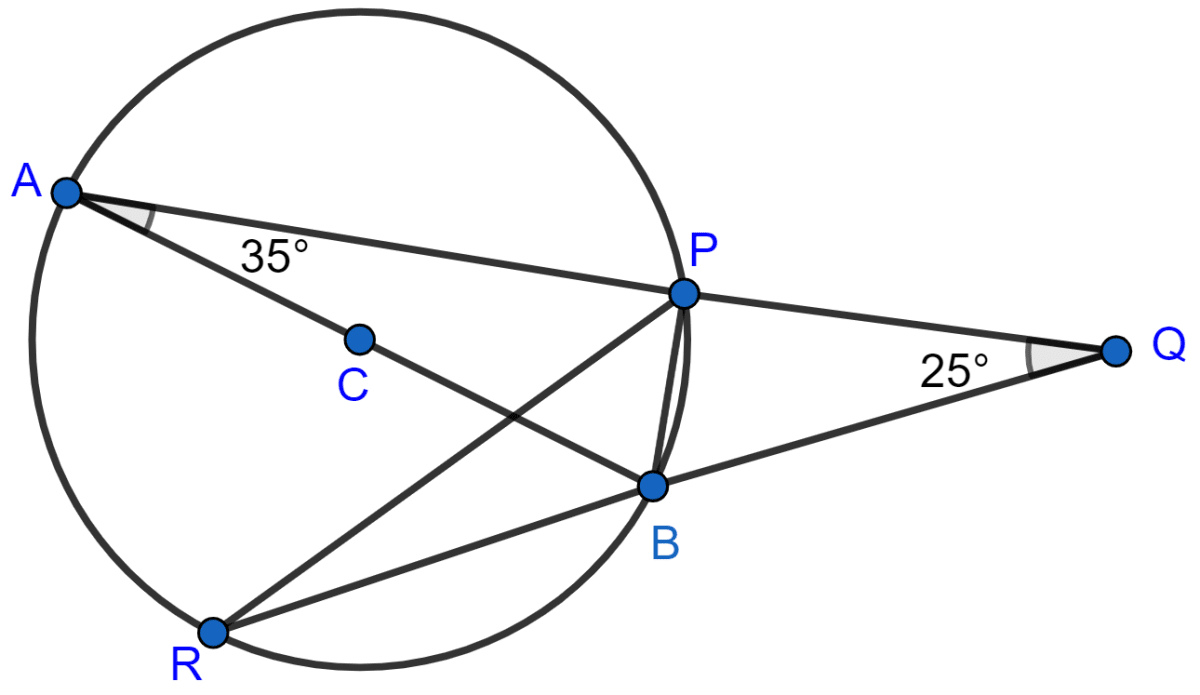
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find :
(i) ∠PRB,
(ii) ∠PBR,
(iii) ∠BPR.
In the given figure, A is the center of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that : ∠BCD = 2∠ABE.
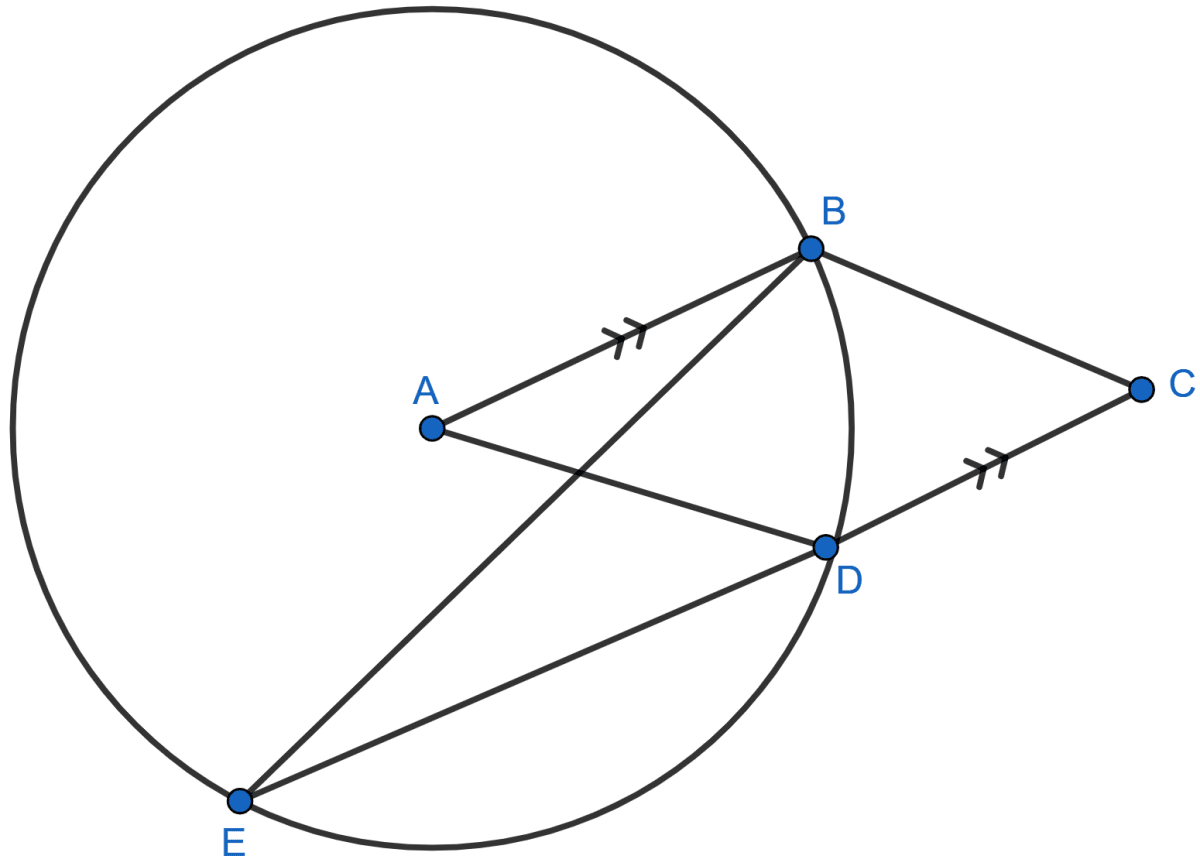
In the given figure, AB = AC = CD and ∠ADC = 38°. Calculate :
(i) Angle ABC
(ii) Angle BEC

In the given figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x.
