Mathematics
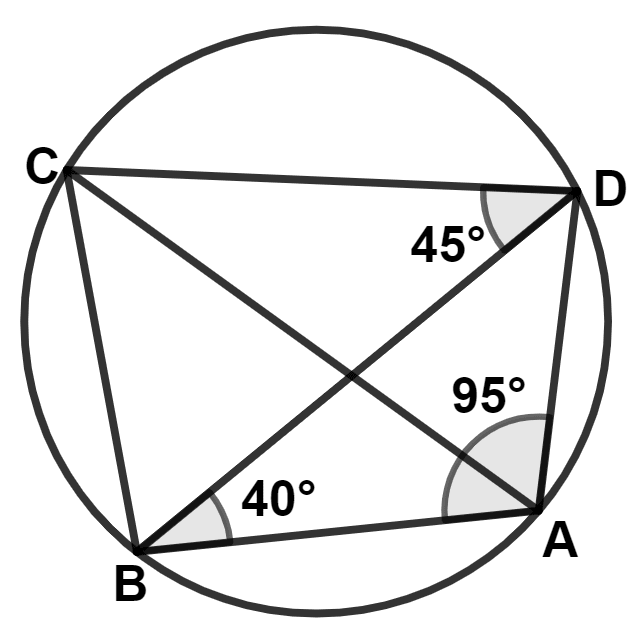
In the given circle, ∠BAD = 95°, ∠ABD = 40° and ∠BDC = 45°.
Assertion (A) : To show that AC is a diameter, the angle ADC or angle ABC need to be proved to be 90°.
Reason (R) : In △ADB,
∠ADB = 180° - 95° - 40° = 45°
∴ Angle ADC = 45° + 45° = 90°
(i) A is true, R is false
(ii) A is true, R is true
(iii) A is false, R is false
(iv) A is false, R is true
Answer
We know that,
Angle in semicircle is a right angle.
If AC is the diameter, then ∠ADC = ∠ABC = 90°.
∴ Assertion (A) is true.
From figure,
In △ADB,
By angle sum property of triangle,
∴ ∠ADB + ∠DBA + ∠BAD = 180°
⇒ ∠ADB + 40° + 95° = 180°
⇒ ∠ADB + 135° = 180°
⇒ ∠ADB = 180° - 135° = 45°.
From figure,
⇒ ∠ADC = ∠ADB + ∠BDC = 45° + 45° = 90°.
∴ Reason (R) is true.
Hence, Option 2 is the correct option.
Related Questions
In the given figure, O is center of the circle and OABC is a rhombus, then :
x° + y° = 180°
x° = y° = 90°
x° + 2y° = 360°
x° = y° = 45°
Arcs AB and BC are of lengths in the ratio 11 : 4 and O is center of the circle. If angle BOC = 32°, the angle AOB is :
64°
88°
128°
132°
In the given figure, AB is the side of regular pentagon and BC is the side of regular hexagon. Angle BAC is :
132°
66°
90°
120°
In the given figure x°, y°, z° and p° are exterior angles of cyclic quadrilateral ABCD, then x° + y° + z° + p° is :
180°
270°
360°
720°
