Mathematics
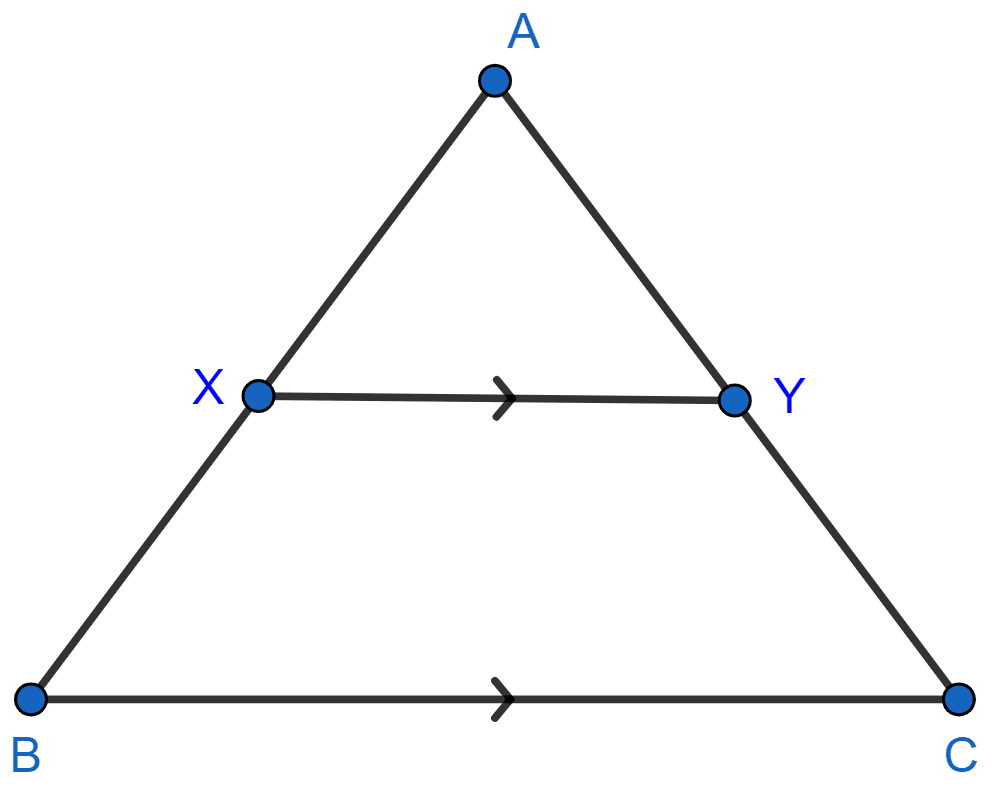
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
Find:
(i)
(ii)
(iii) XY
Similarity
16 Likes
Answer
(i) By basic proportionality theorem,
A line drawn parallel to a side of triangle divides the other two sides proportionally.
Hence,
(ii) Given,
Let AY = 2x and YC = x.
From figure,
AC = AY + YC = 2x + x = 3x.
.
Hence, .
(iii) In △AXY and △ABC,
∠AXY = ∠ABC [Corresponding angles are equal]
∠A = ∠A [Common]
∴ △AXY ~ △ABC.
Since, corresponding sides of similar triangle are proportional to each other.
Hence, XY = 12 cm.
Answered By
8 Likes
Related Questions
In triangle ABC, ∠B = 90° and in triangle ADE, ∠D = 90°.

Statement (1) : .
Statement (2) : Triangle AED and ACB are similar.
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Area of triangle ADE = 9 cm2 and area of trapezium DBCE = 16 cm2.
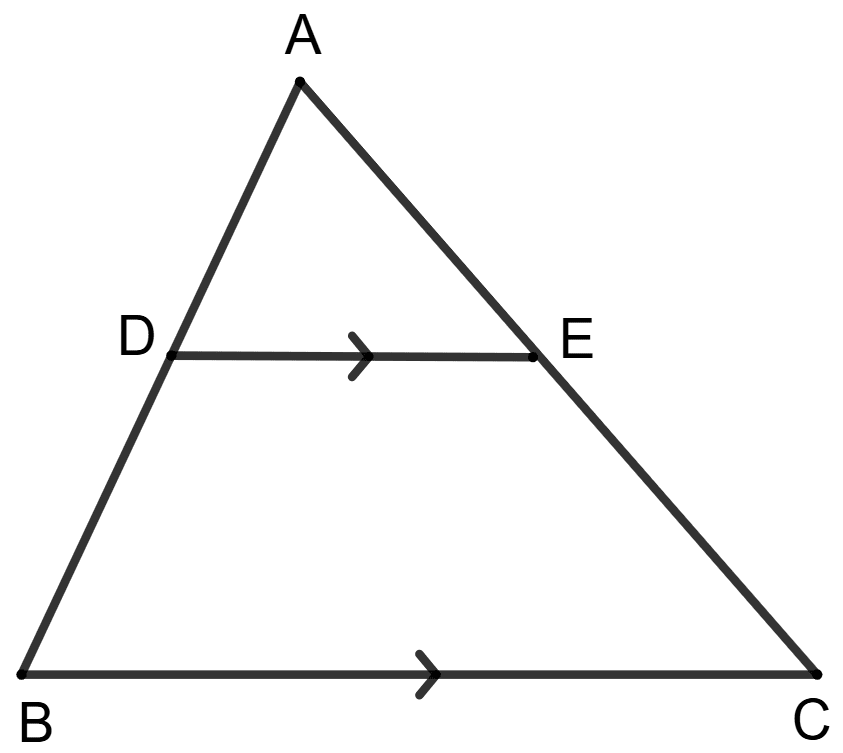
Statement (1) : .
Statement (2) : .
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
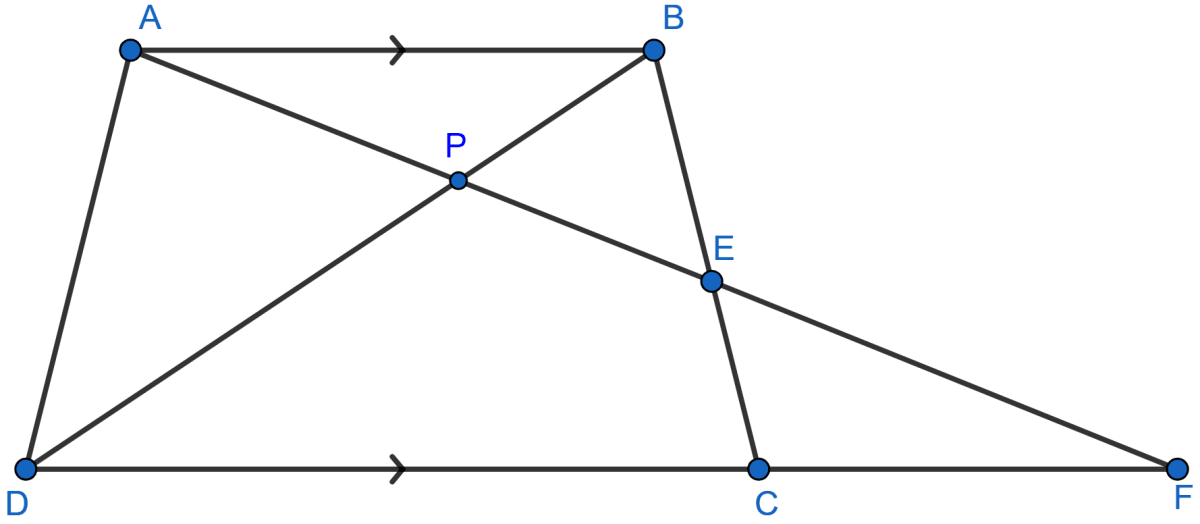
In the following figure, ABCD is a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm,
Calculate :
(i) EC (ii) AF (iii) PE
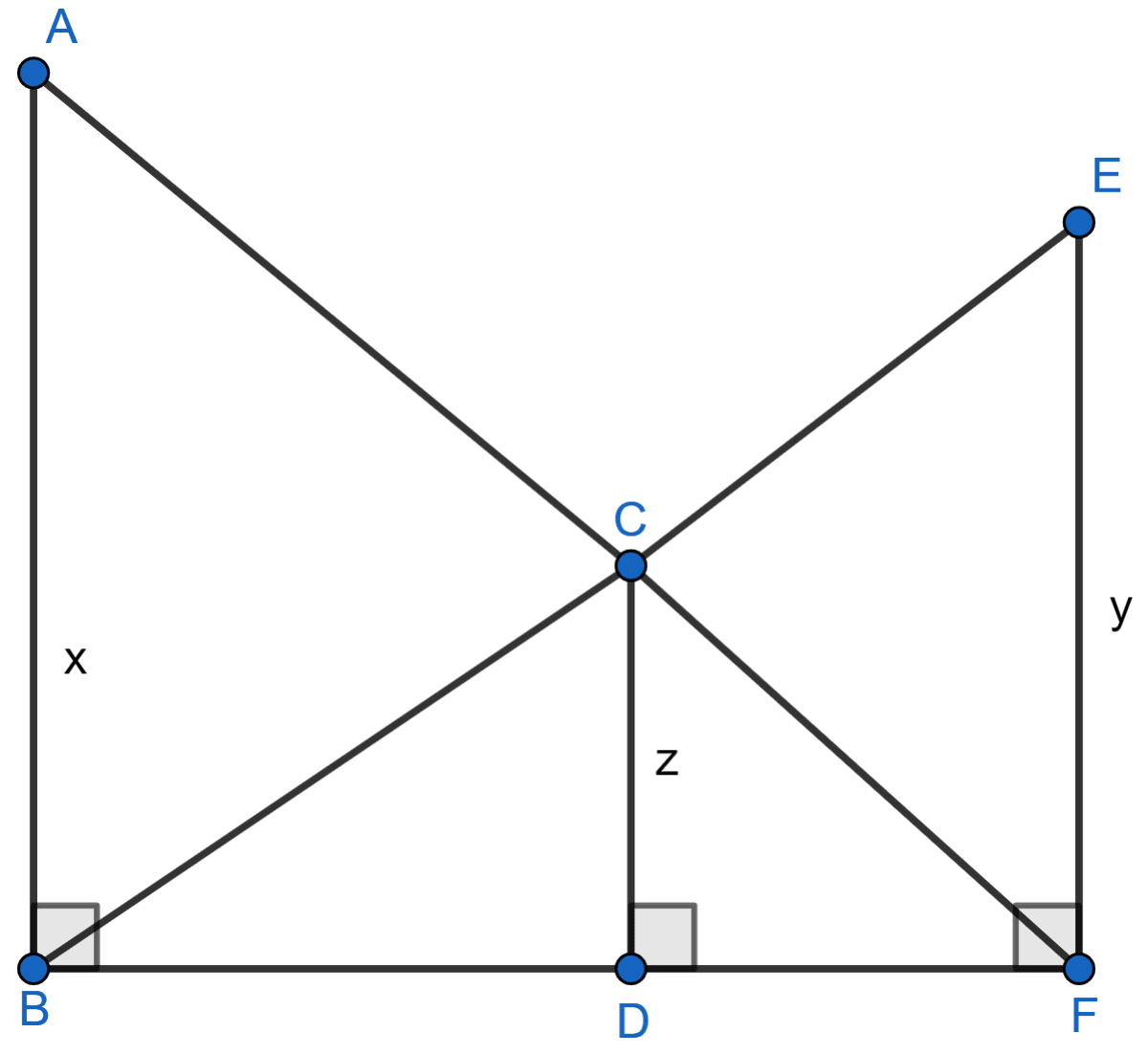
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
If AB = x and, CD = z unit and EF = y unit, prove that: