Mathematics
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with center O.
Calculate the values of :
(i) ∠QOP
(ii) ∠QCP

Circles
8 Likes
Answer
(i) Given,
PQ = QR
∴ ∠PRQ = ∠QPR [Angles opposite to equal sides are equal in a triangle.]
In △PQR,
⇒ ∠PRQ + ∠QPR + ∠RQP = 180°
⇒ ∠PRQ + ∠PRQ + 68° = 180°
⇒ 2∠PRQ = 180° - 68°
⇒ 2∠PRQ = 112°
⇒ ∠PRQ =
⇒ ∠PRQ = 56°.
We know that,
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
∴ ∠QOP = 2∠PRQ = 2 x 56 = 112°.
Hence, ∠QOP = 112°.
(ii) We know that,
A tangent line is always at a right angle to the radius of the circle at the point of tangency.
∴ ∠OPC = 90° and ∠OQC = 90°.
In quadrilateral OQCP,
⇒ ∠QOP + ∠OPC + ∠OQC + ∠QCP = 360° [Angle sum property of quadrilateral]
⇒ 112° + 90° + 90° + ∠QCP = 360°
⇒ ∠QCP = 360° - 292° = 68°.
Hence, ∠QCP = 68°.
Answered By
5 Likes
Related Questions
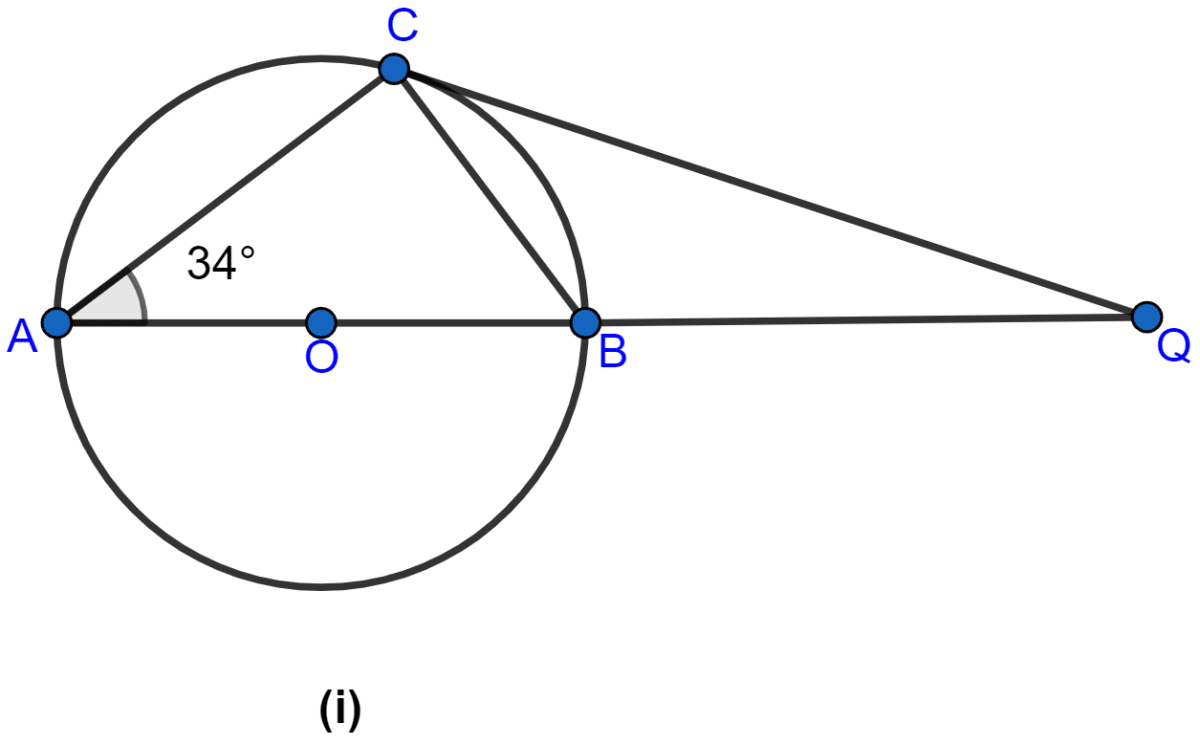
In the figure (i) given below, AB is a diameter. The tangent at C meets AB produced at Q, ∠CAB = 34°. Find :
(i) ∠CBA
(ii) ∠CQA
In the given figure, O is the center of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find :
(i) ∠BOD
(ii) ∠BPD

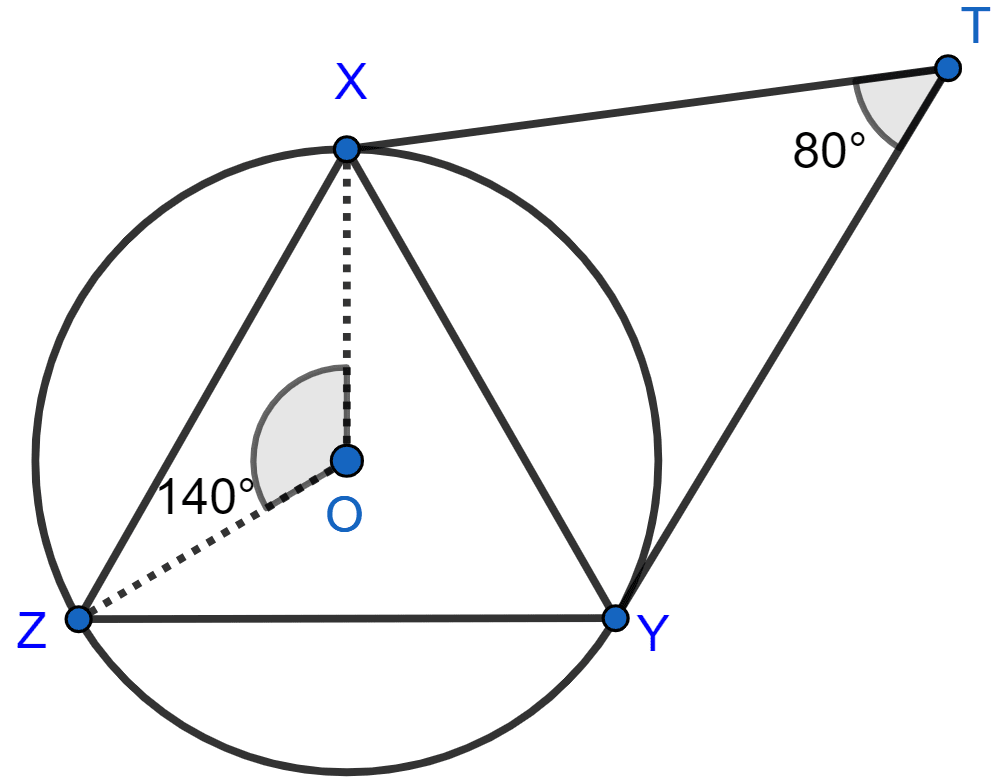
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
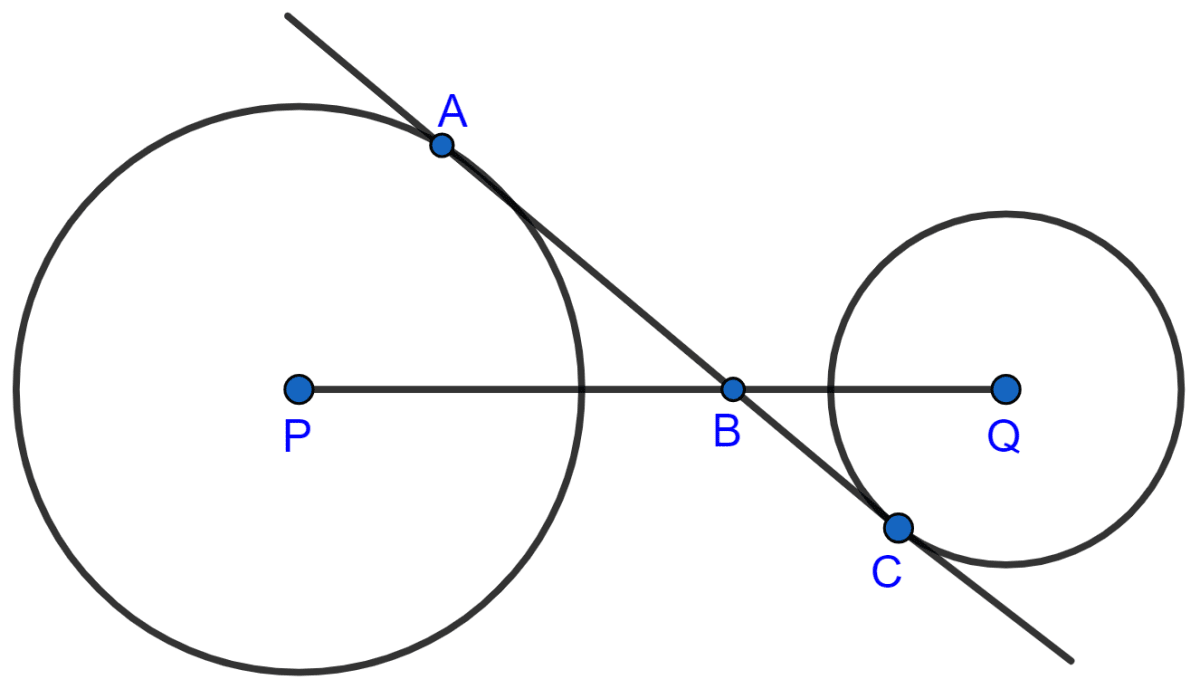
In the figure, given below, AC is a transverse common tangent to two circles with centers P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.