Mathematics
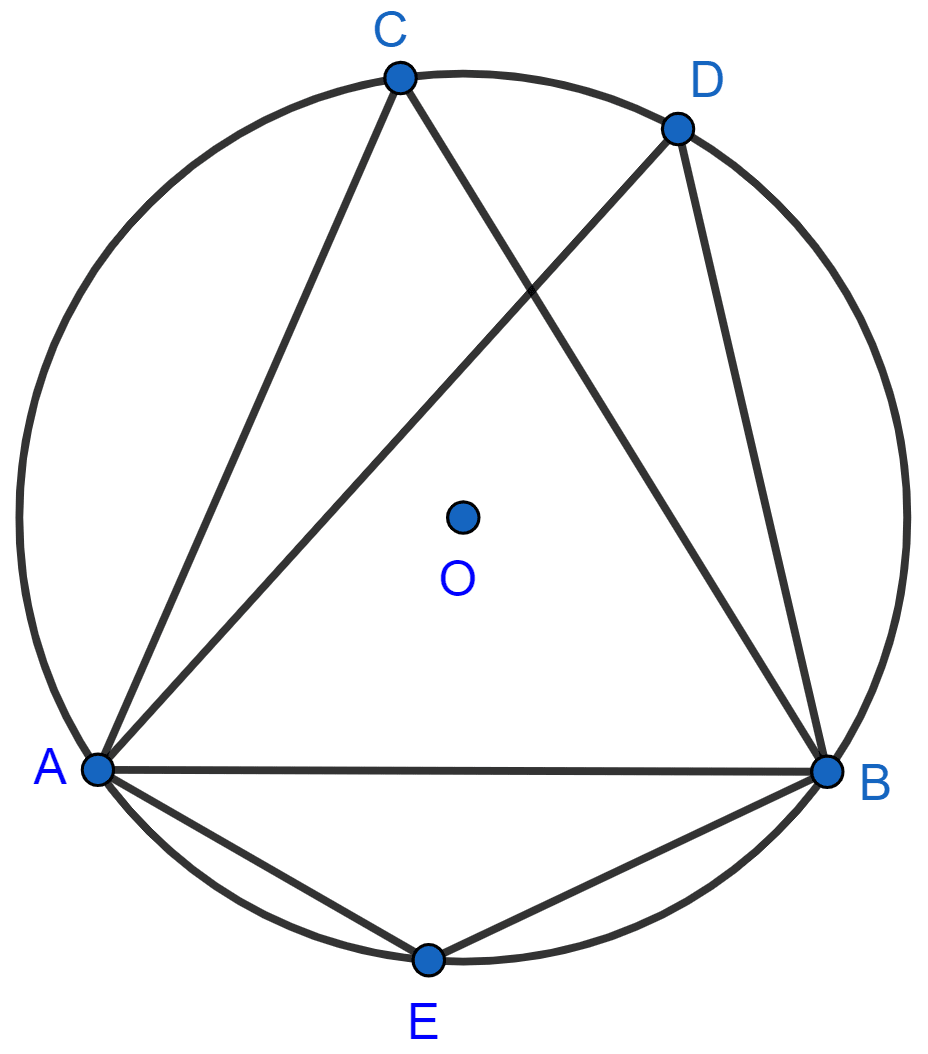
In the following figure, O is the centre of the circle and ΔABC is equilateral.
Find:
(i) ∠ADB, (ii) ∠AEB.
Circles
13 Likes
Answer
(i) We know that each angle in an equilateral triangle = 60°.
∴ ∠ACB = 60°
As angles in same segment are equal.
∴ ∠ADB = ∠ACB = 60°.
Hence, ∠ADB = 60°.
(ii) Join OA and OB.
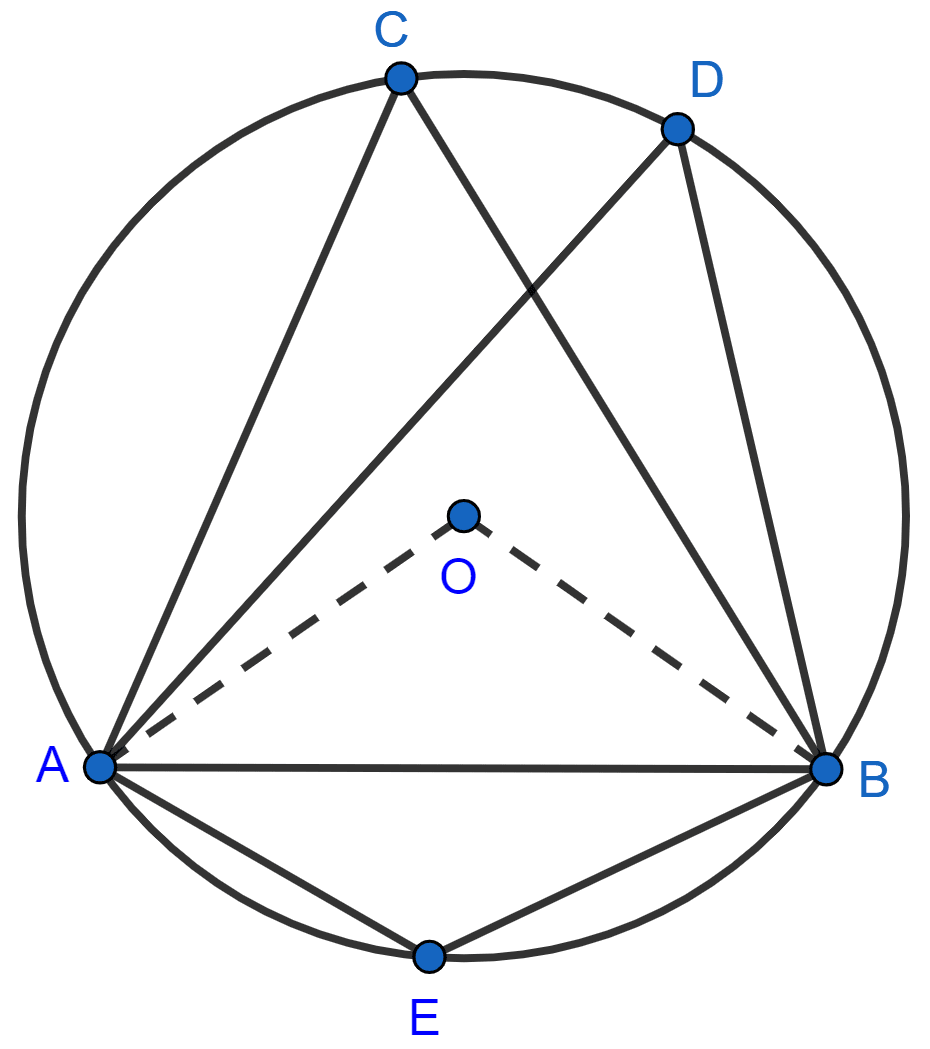
We know that,
Angle at the center is double the angle at the circumference subtended by the same chord.
∴ ∠AOB = 2∠ACB = 2 x 60° = 120°.
∴ ∠AEB = Reflex ∠AOB
= (360° - 120°) =
= 120°.
Hence, ∠AEB = 120°.
Answered By
9 Likes
Related Questions
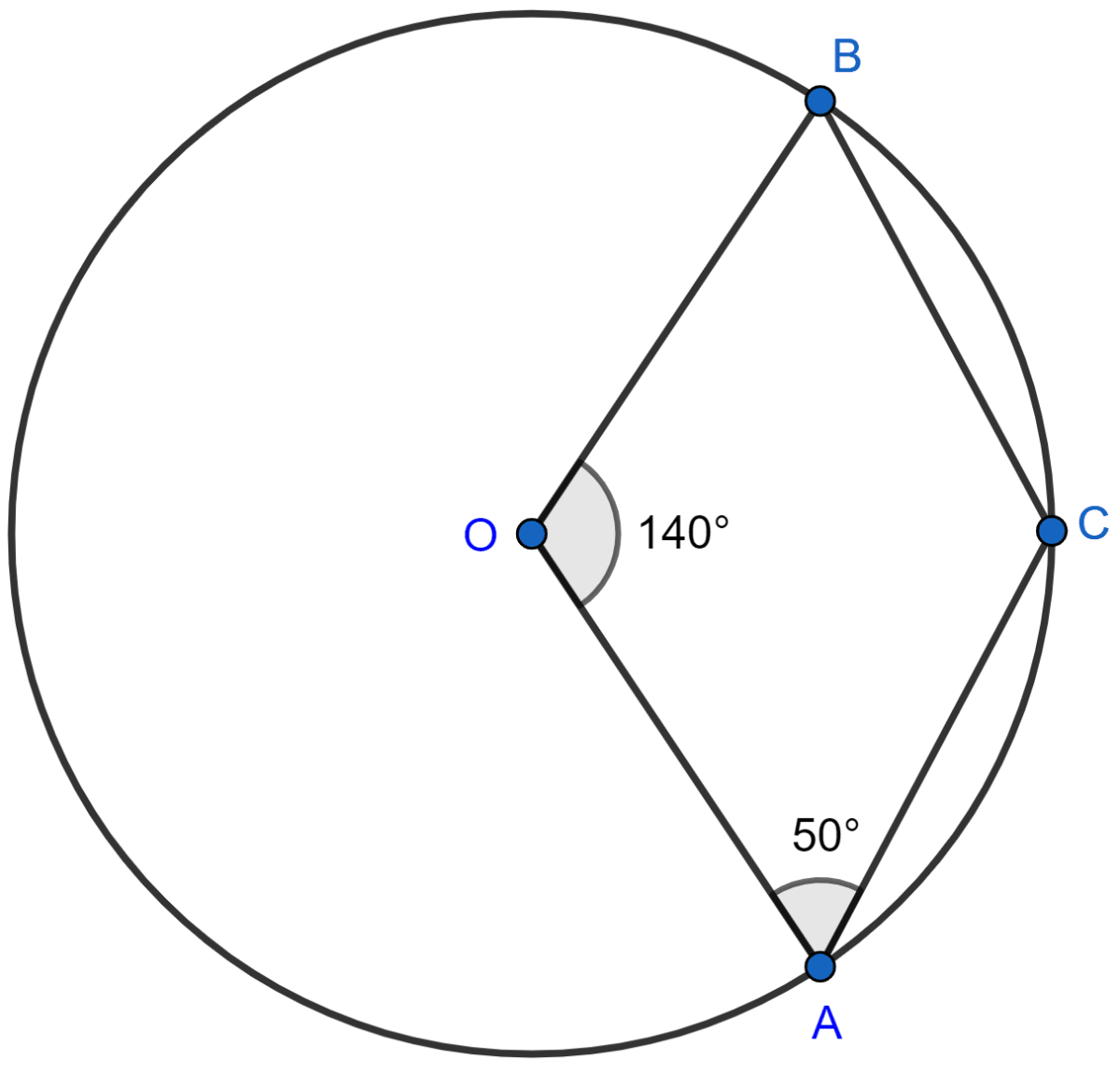
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find :
(i) ∠ACB,
(ii) ∠OBC,
(iii) ∠OAB,
(iv) ∠CBA.
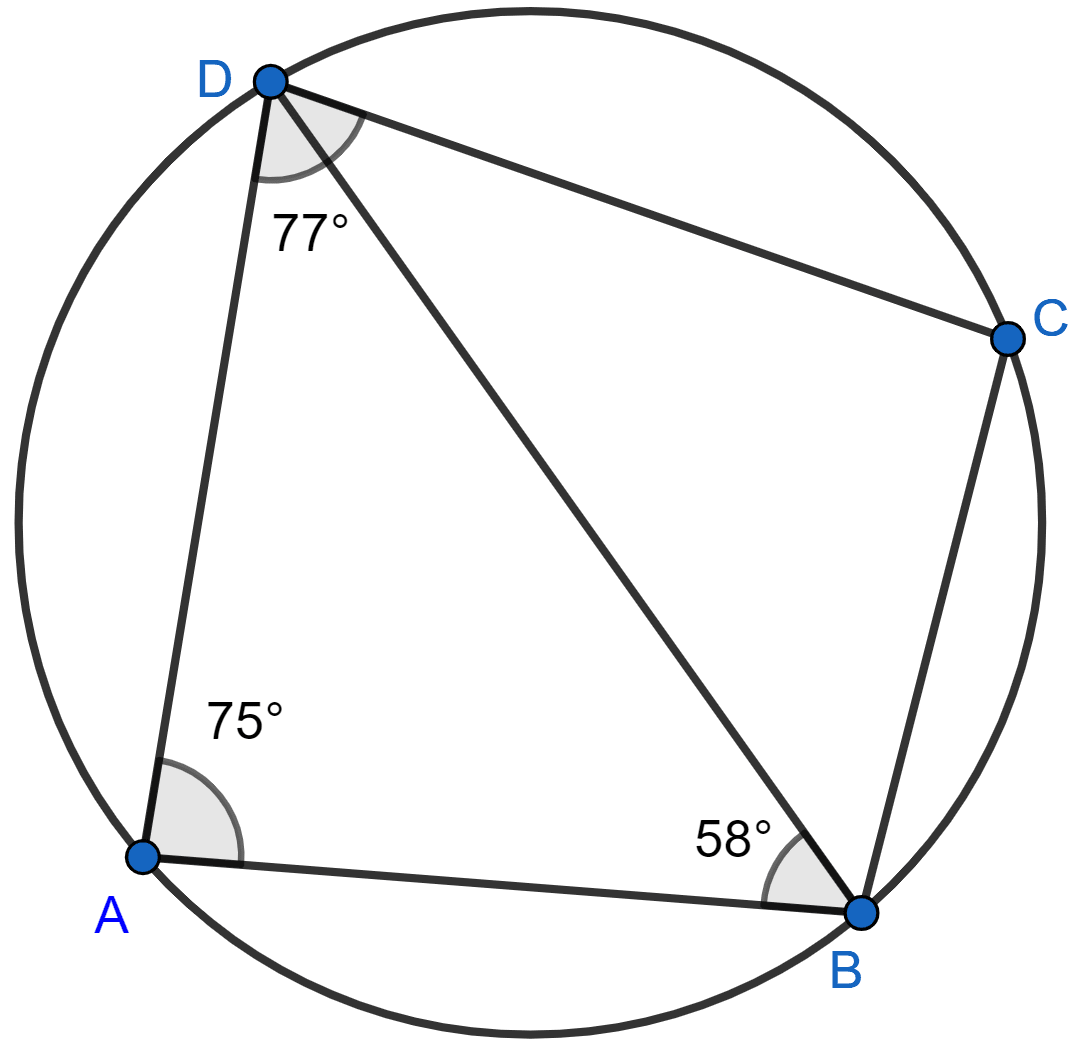
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find :
(i) ∠BDC,
(ii) ∠BCD,
(iii) ∠BCA.
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°, find ∠BAC.

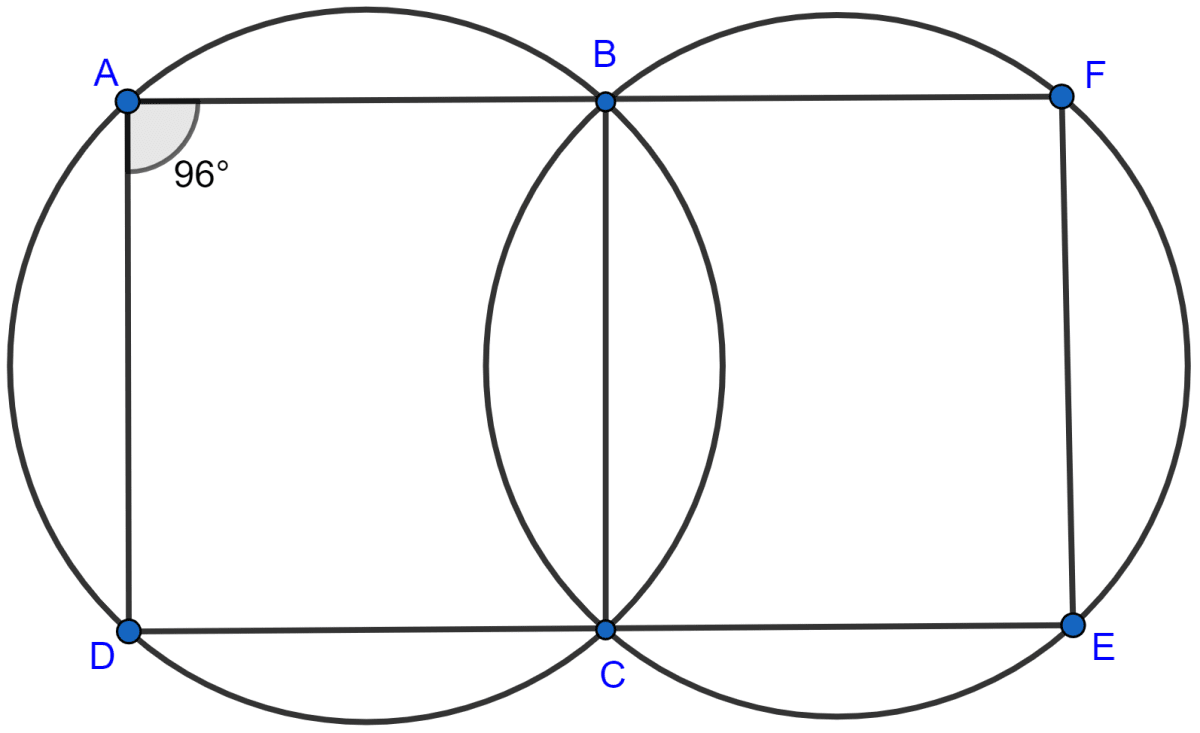
In the following figure,
(i) if ∠BAD = 96°, find ∠BCD and ∠BFE.
(ii) Prove that AD is parallel to FE.