Mathematics
Answer

In △ABC and △CDE,
∠ACB = ∠DCE (Vertically opposite angles)
∠BAC = ∠CED (Given)
BC = CD (Given)
∴ △ABC ≅ △CDE (By AAS axiom)
We know that corresponding parts of congruent triangles are equal.
∴ DE = AB
⇒ 2y + 3 = 25
⇒ 2y = 22
⇒ y = 11.
Given, BC = CD
⇒ 3x - 7 = 32
⇒ 3x = 32 + 7
⇒ 3x = 39
⇒ x = 13.
Hence, x = 13 and y = 11.
Related Questions
In the figure (2) given below, AB || DC and ∠C = ∠D. Prove that
(i) AD = BC
(ii) AC = BD.

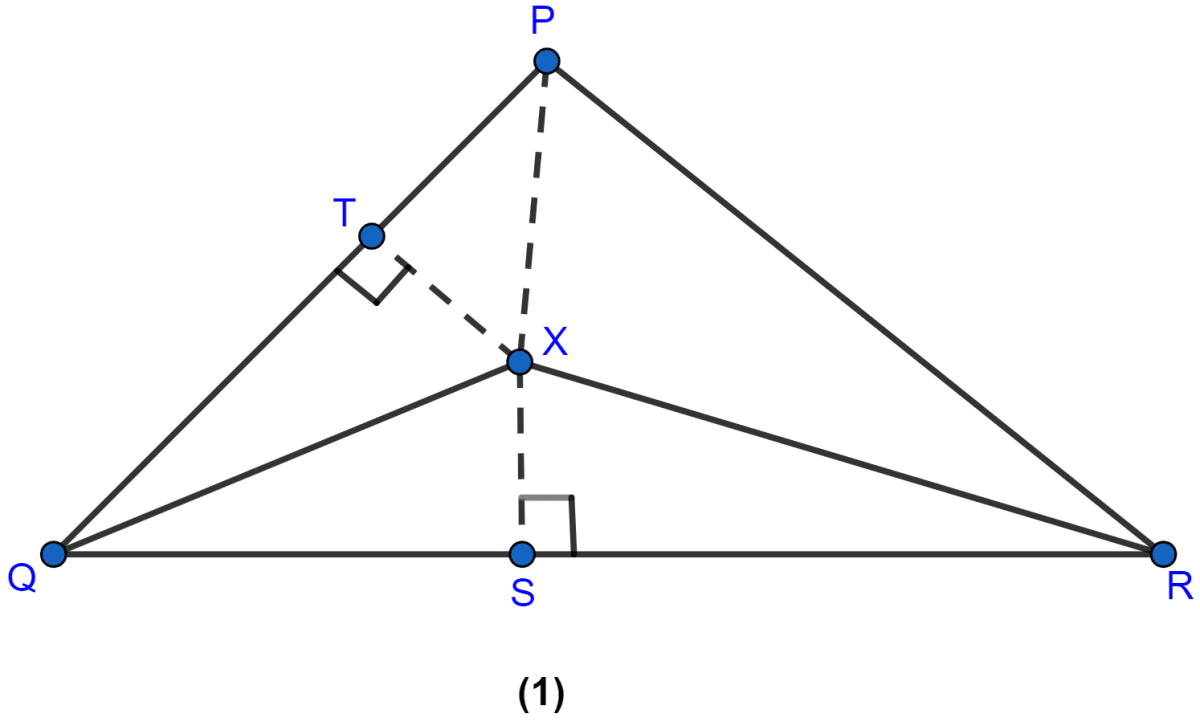
In the figure (1) given below, QX, RX are bisectors of angles PQR and PRQ respectively of △PQR. If XS ⊥ QR and XT ⊥ PQ, prove that
(i) △XTQ ≅ △XSQ
(ii) PX bisects the angle P.
In the figure (3) given below, BA || DF and CA || EG and BD = EC. Prove that
(i) BG = DF
(ii) EG = CF.

In the following figure, find the values of x and y.