Mathematics
In the figure (ii) given below, there are five squares each of side 2 cm.
(i) Find the radius of the circle.
(ii) Find the area of the shaded region. (Take π = 3.14).

Mensuration
10 Likes
Answer
(i) Let O be the center of the circle.
B be the mid-point of side of square.
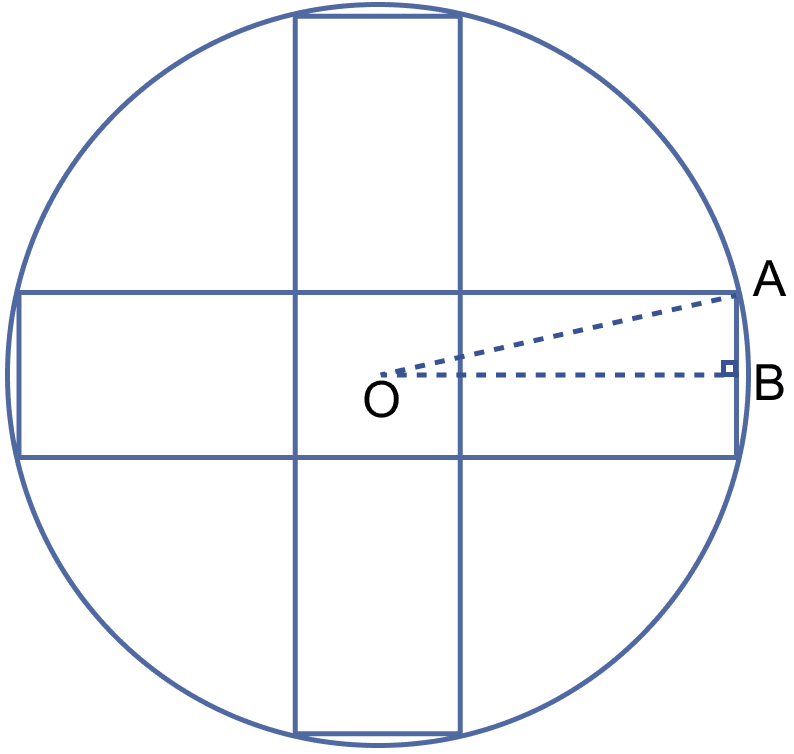
From figure,
OB = 2 + 1 = 3 cm
AB = 1 cm
Using Pythagoras theorem,
OA =
OA = .
So, the radius of the circle = cm.
Hence, the radius of circle = cm.
(ii) We know that,
Area of the circle = πr2.
= 3.14 ×
= 3.14 × 10
= 31.4 cm2.
Area of 5 square of side 2 cm each = 22 × 5
= 4 × 5
= 20 cm2.
So, the area of shaded portion = 31.4 – 20 = 11.4 cm2.
Hence, area of shaded portion = 11.4 cm2.
Answered By
5 Likes
Related Questions
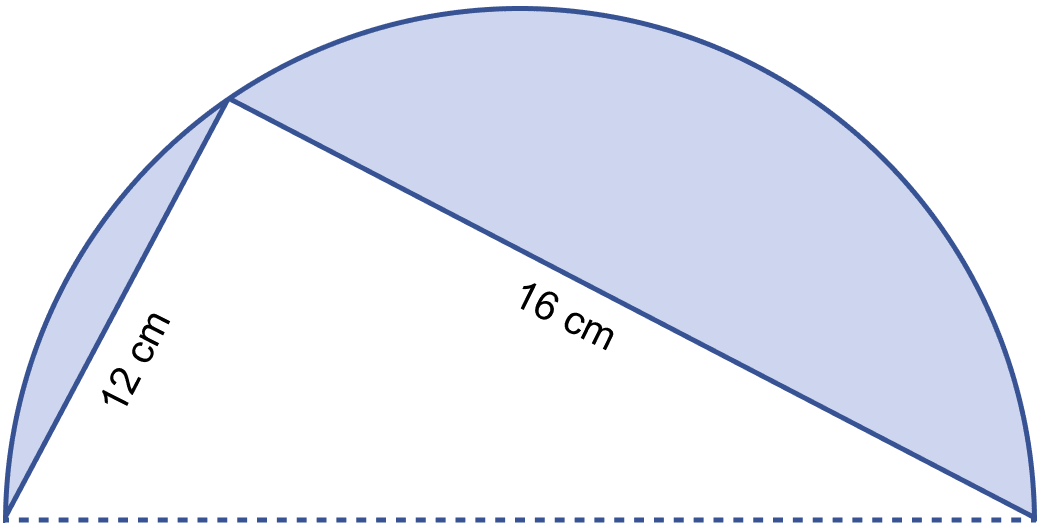
In the adjoining figure, O is the center of a circular arc and AOB is a line segment. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
In the figure (i) given below, the radius is 3.5 cm. Find the perimeter of the quarter of the circle.

In the figure (i) given below, a piece of cardboard in the shape of a quadrant of a circle of radius 7 cm is bounded by the perpendicular radii OX and OY. Points A and B lie on OX and OY respectively such that OA = 3 cm and OB = 4 cm. The triangular part OAB is removed. Calculate the area and the perimeter of the remaining piece.

In the figure (ii) given below, ABCD is a square. Points A, B, C and D are centres of quadrants of circles of the same radius. If the area of the shaded portion is cm2, find the radius of the quadrants.