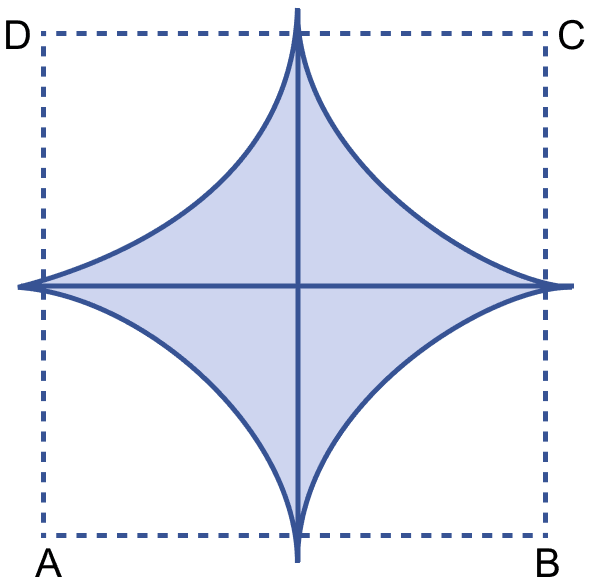
In the figure (ii) given below, ABCD is a square. Points A, B, C and D are centres of quadrants of circles of the same radius. If the area of the shaded portion is $21\dfrac{3}{7}$ cm², find the radius of the quadrants.

Let radius be r cm of each quadrant.

Area of each quadrant = $\dfrac{πr^2}{4}$

So, area of 4 quadrants = $4 \times \dfrac{πr^2}{4} = πr^2$

From figure,

Side of square = r + r = 2r

Area of square ABCD = (Side)² = (2r)² = 4r².

Area of shaded region = Area of square ABCD - Area of 4 quadrants

$\Rightarrow 21\dfrac{3}{7} = 4r^2 - πr^2 \\[1em] \Rightarrow \dfrac{150}{7} = 4r^2 - πr^2 \\[1em] \Rightarrow \dfrac{150}{7} = r^2(4 - π) \\[1em] \Rightarrow \dfrac{150}{7} = r^2\Big(4 - \dfrac{22}{7}\Big) \\[1em] \Rightarrow \dfrac{150}{7} = r^2\Big(\dfrac{28 - 22}{7}\Big) \\[1em] \Rightarrow \dfrac{150}{7} = r^2 \times \dfrac{6}{7} \\[1em] \Rightarrow r^2 = \dfrac{150 \times 7}{6 \times 7} \\[1em] \Rightarrow r^2 = 25 \\[1em] \Rightarrow r = 5 \text{ cm}.$

Hence, radius of quadrant = 5 cm.