Mathematics
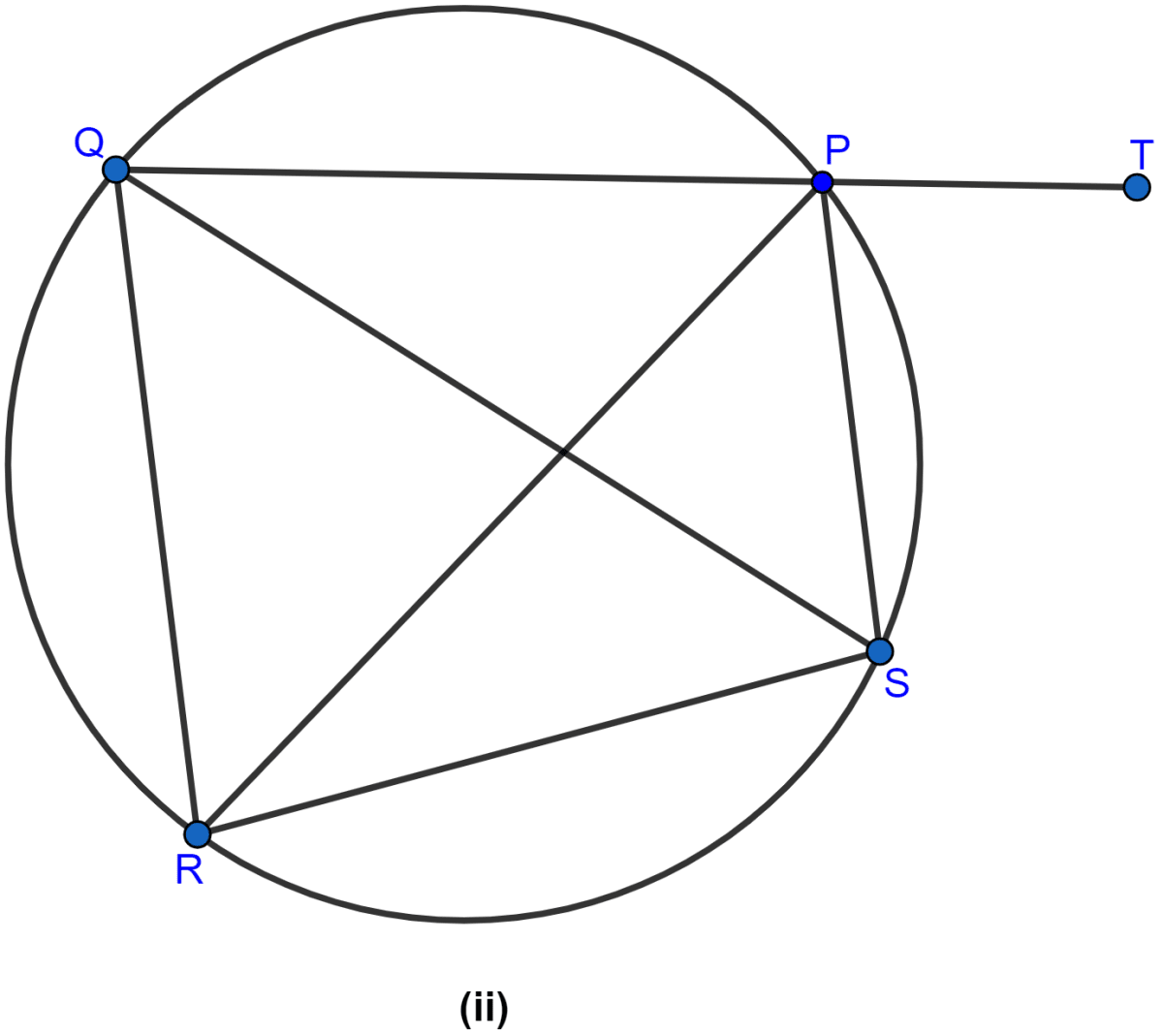
In the figure (ii) given below, SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that SQ = RS.
Circles
55 Likes
Answer
Since, SP is the bisector of the angle ∠RPT.
So, ∠RPS = ∠SPT
From figure,
∠RPS = ∠RQS (As angle in same segment are equal)
Given, PQRS is a cyclic quadrilateral.
∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
∠QRS = ∠SPT
∴ ∠QRS = ∠RPS
or,
∠QRS = ∠RQS
In △QRS,
∠QRS = ∠RQS
∴ SQ = RS (As sides opposite to equal angles are equal.)
Hence, proved that SQ = RS.
Answered By
35 Likes
Related Questions
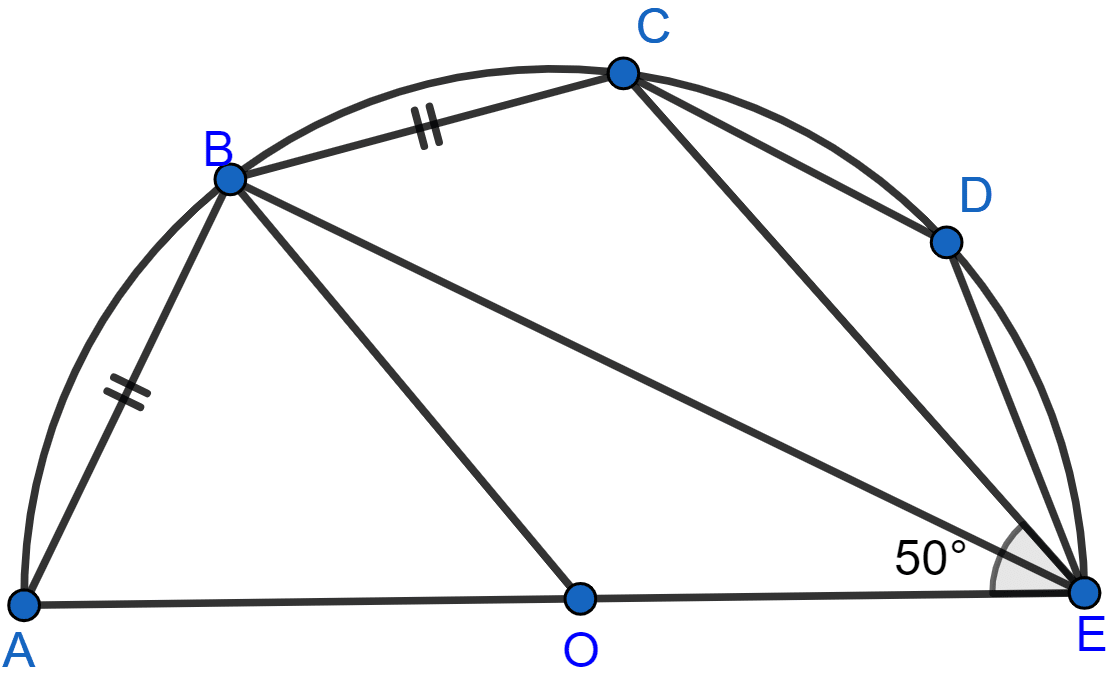
In the adjoining figure, O is the center and AOE is the diameter of the semicircle ABCDE. If AB = BC and ∠AEB = 50°, find :
(i) ∠CBE
(ii) ∠CDE
(iii) ∠AOB.
Prove that OB is parallel to EC.
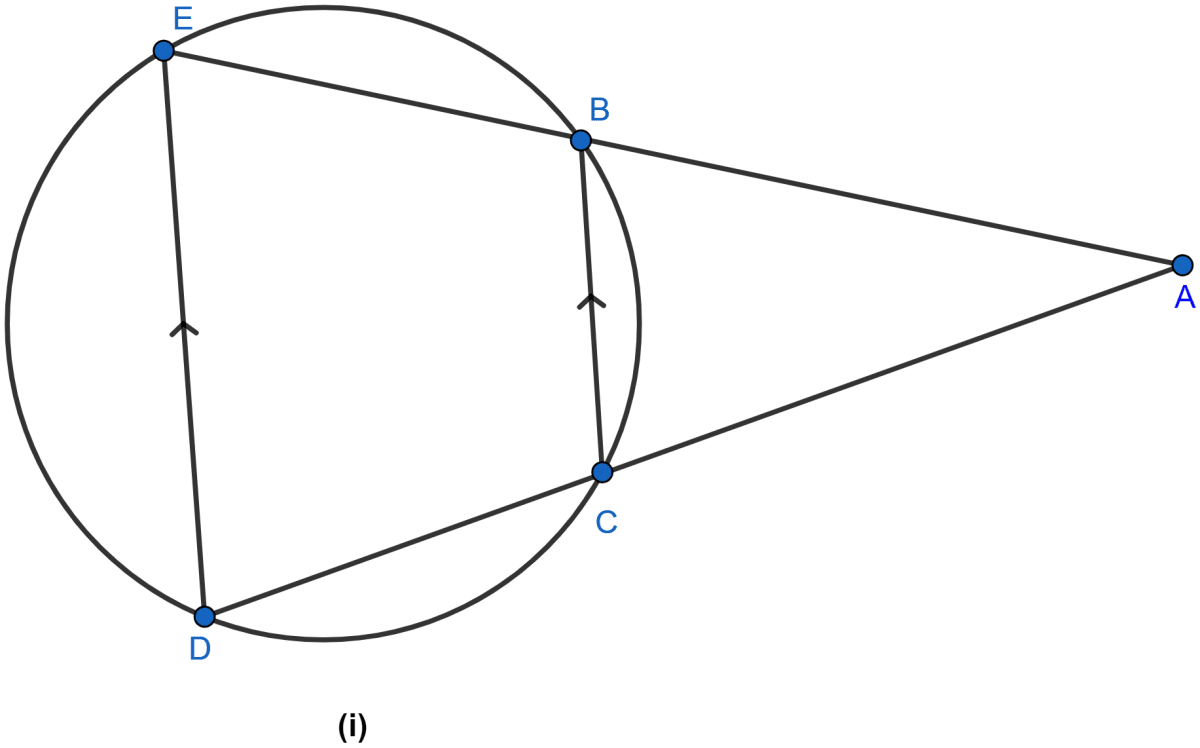
In the figure (i) given below, ED and BC are two parallel chords of the circle and ABE, ACD are two st. lines. Prove that AED is an isosceles triangle.
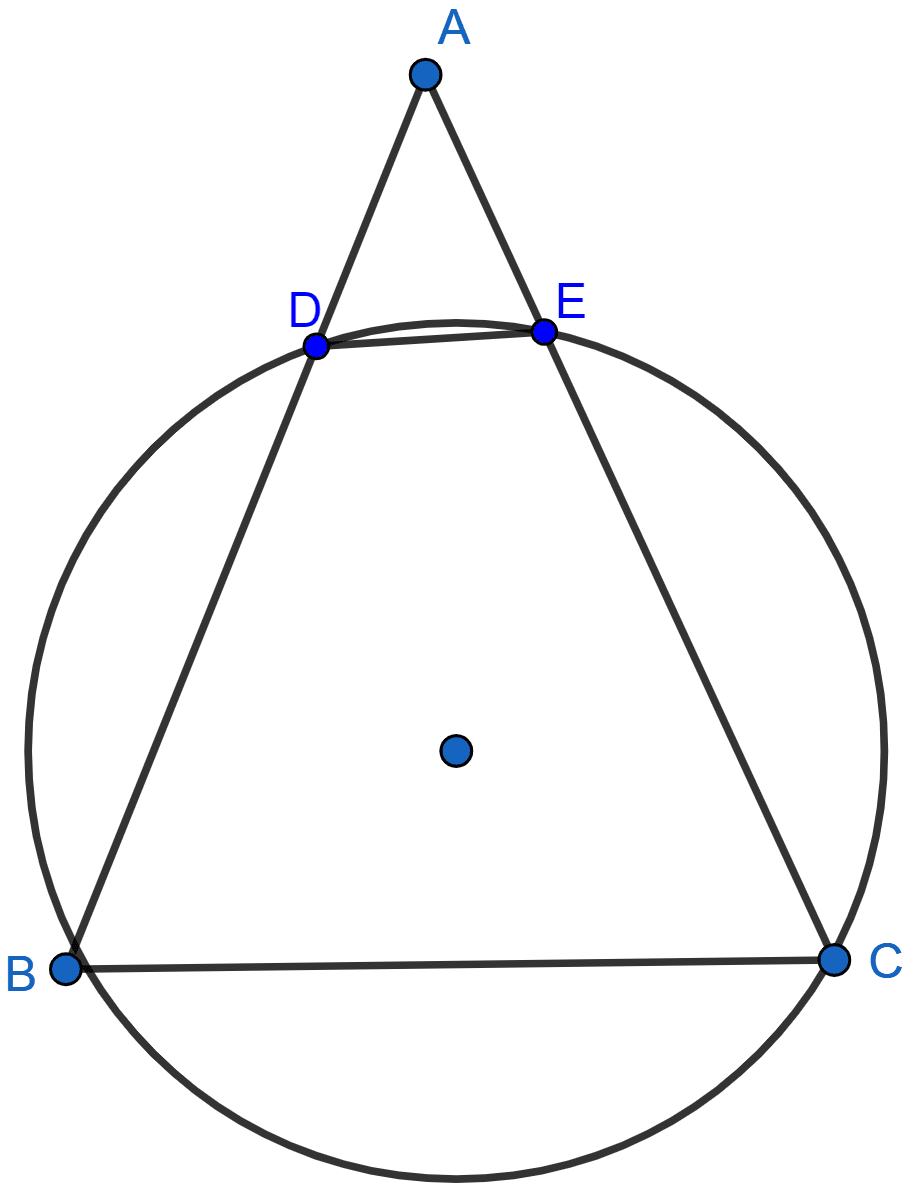
In the adjoining figure, ABC is an isosceles triangle in which AB = AC and circle passing through B and C intersects sides AB and AC at points D and E. Prove that DE || BC.
Prove that a cyclic parallelogram is a rectangle.