Mathematics
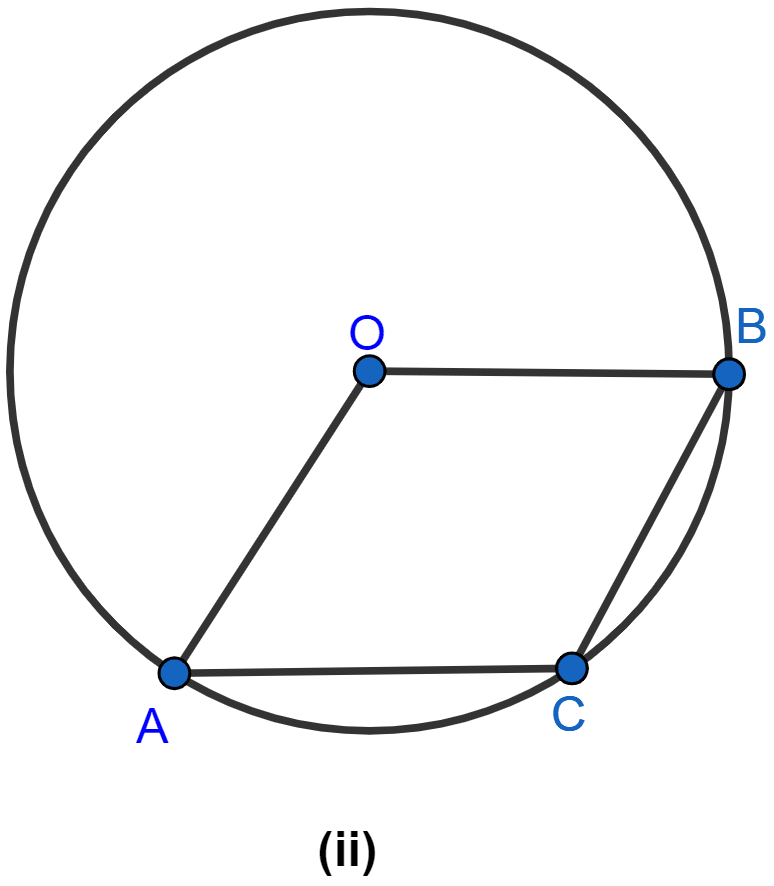
In the figure (ii) given below, O is the circumcenter of triangle ABC in which AC = BC. Given that ∠ACB = 56°, calculate
(i) ∠CAB
(ii) ∠OAC.
Circles
67 Likes
Answer
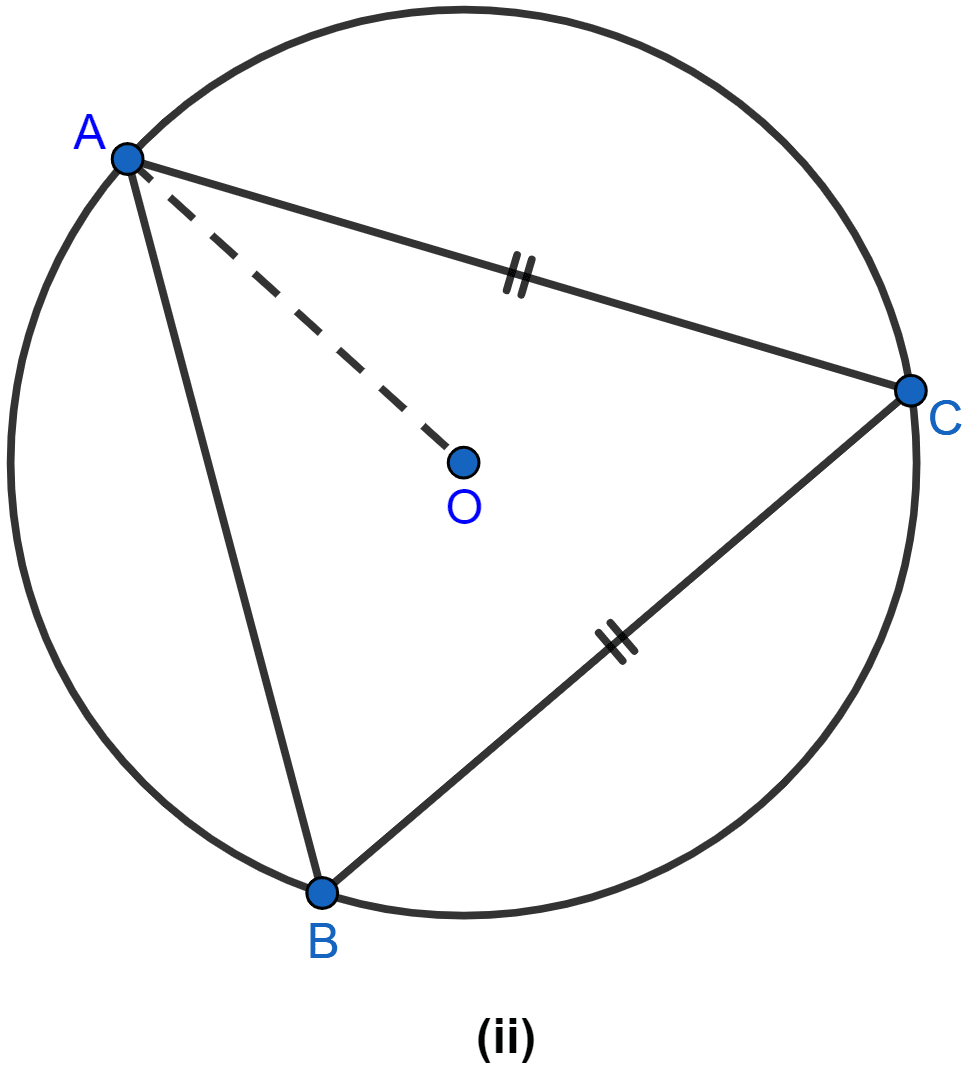
(i) From figure,
AC = BC so,
∠CBA = ∠CAB (As angles of equal sides are equal)
In △ABC,
∠CAB + ∠CBA + ∠ACB = 180°
2∠CAB + 56° = 180°
2∠CAB = 180° - 56°
2∠CAB = 124°
∠CAB = 62°.
Hence, ∠CAB = 62°.
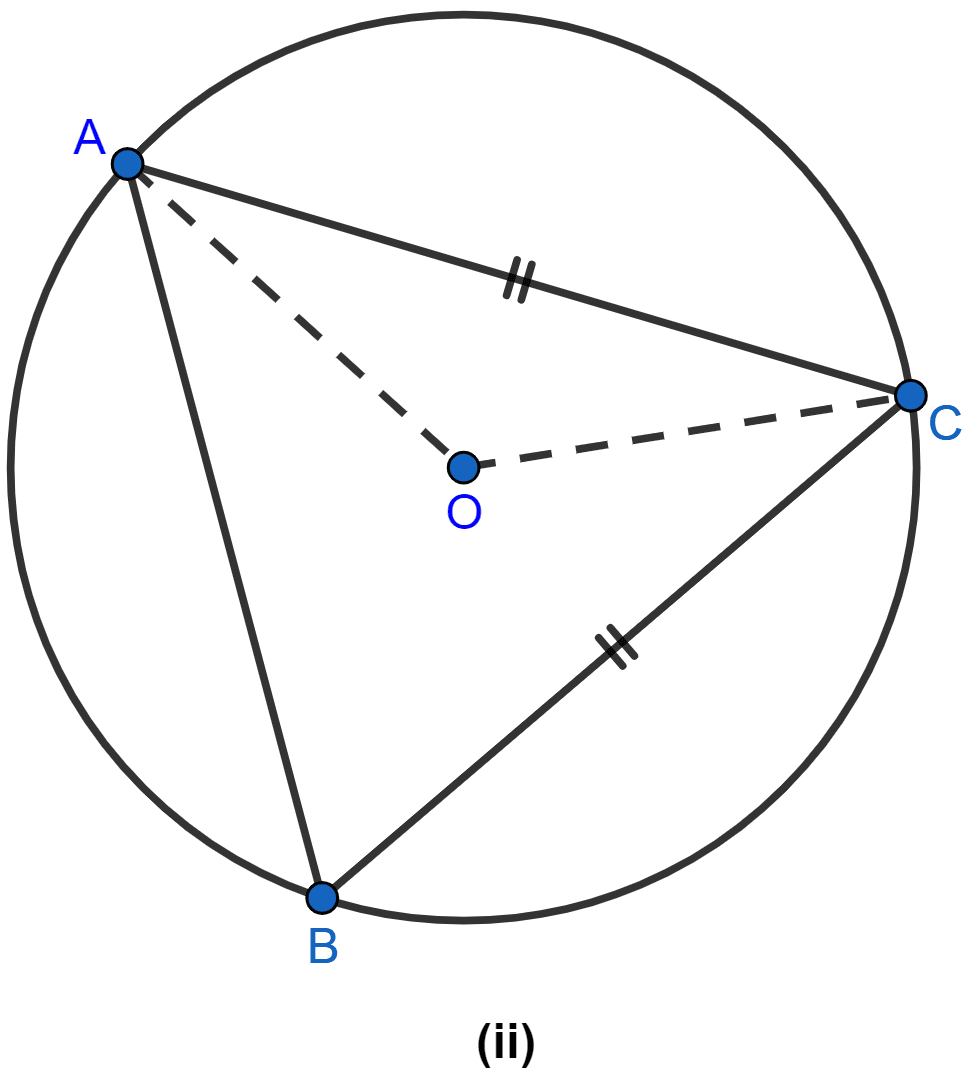
(ii) OC is the radius of the circle. OC bisects ∠ACB.
∠OCA = ∠ACB = 56° = 28°.
Now in △OCA,
OA = OC (Radius of the same circle)
∠OAC = ∠OCA = 28°.
Hence, ∠OAC = 28°.
Answered By
38 Likes
Related Questions
In the figure (ii) given below, it is given that ∠ABC = 40° and AD is a diameter of the circle. Calculate ∠DAC.

In the figure (i) given below, P and Q are centers of two circles intersecting at B and C. ACD is a straight line. Calculate the value of x.

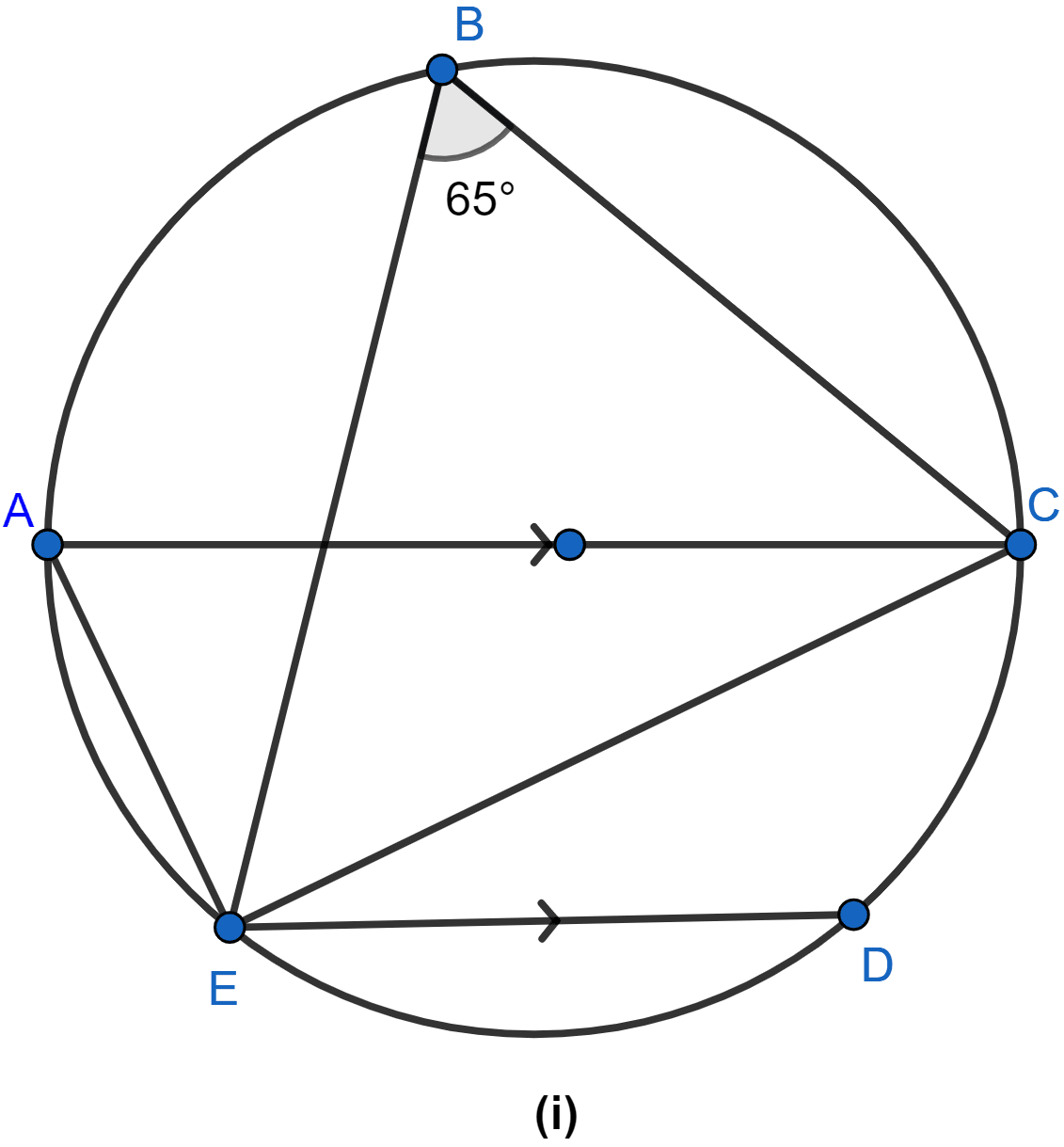
In the figure (i) given below, chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
In the figure (ii) given below, C is a point on the minor arc AB of the circle with centre O. Given ∠ACB = p°, ∠AOB = q°, express q in terms of p. Calculate p if OACB is a parallelogram.