Mathematics
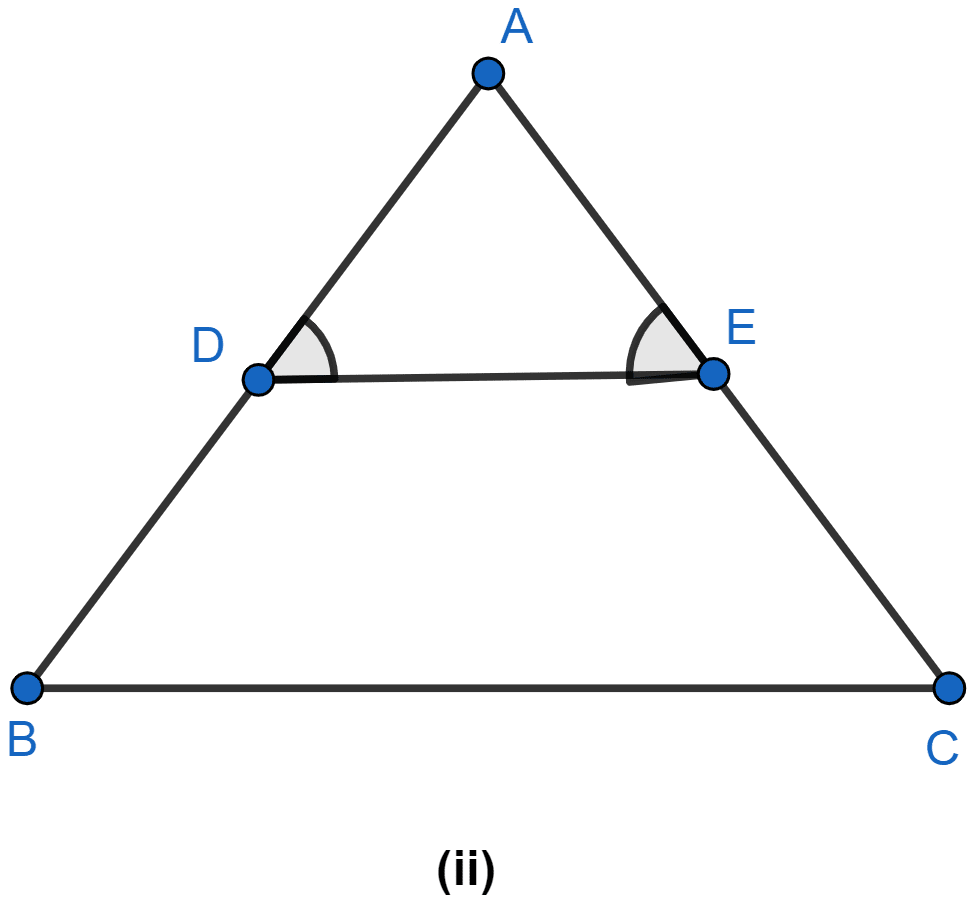
In the figure (ii) given below, ∠D = ∠E and . Prove that ABC is an isosceles triangle.
Similarity
52 Likes
Answer
Given, ∠D = ∠E
So, AD = AE [Sides opposite to equal angles]
Given,
Hence, by basic proportionality theorem, DE is parallel to BC.
As AD = AE so in order to satisfy Eq 1, DB = EC.
AB = AD + DB = AE + EC
and AC = AE + EC.
Hence, AB = AC which means ABC is an isosceles triangle.
Answered By
35 Likes
Related Questions
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5cm, BR = 6 cm and PB = 4 cm. Is AB || QR ? Give reasons for your answer.
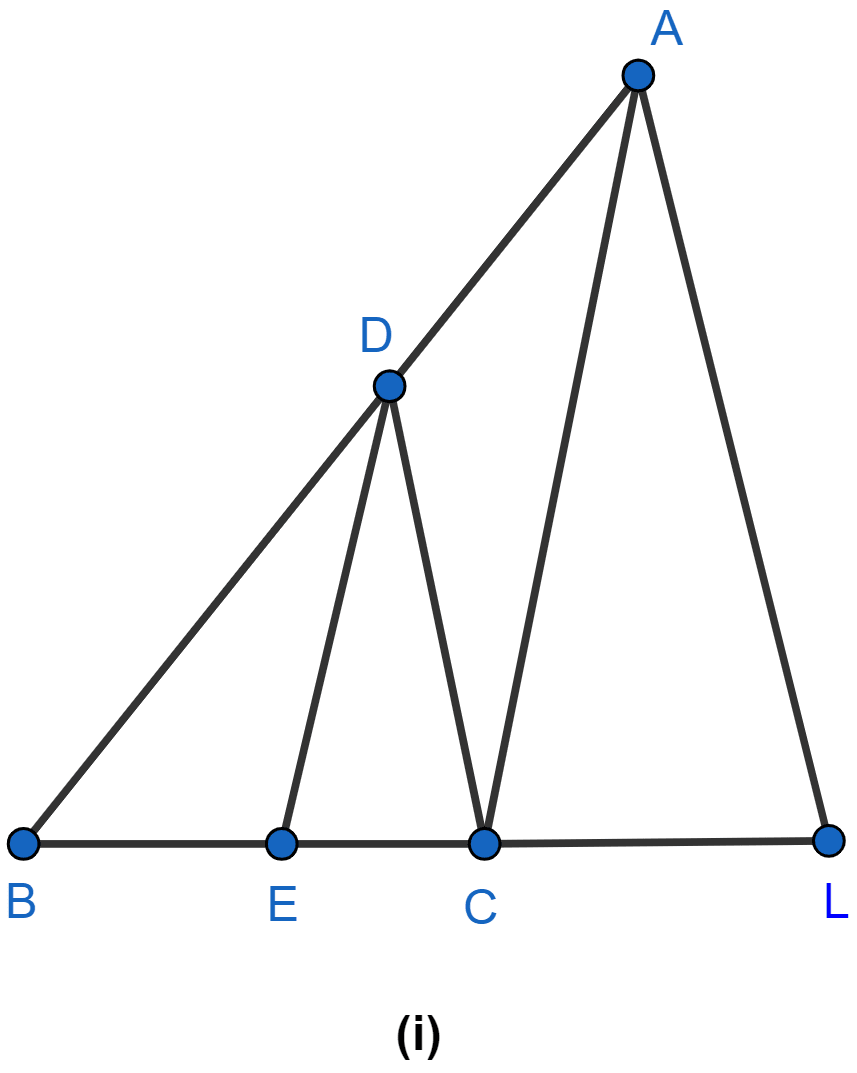
In the figure (i) given below, CD || LA and DE || AC. Find the length of CL if BE = 4 cm and EC = 2 cm.
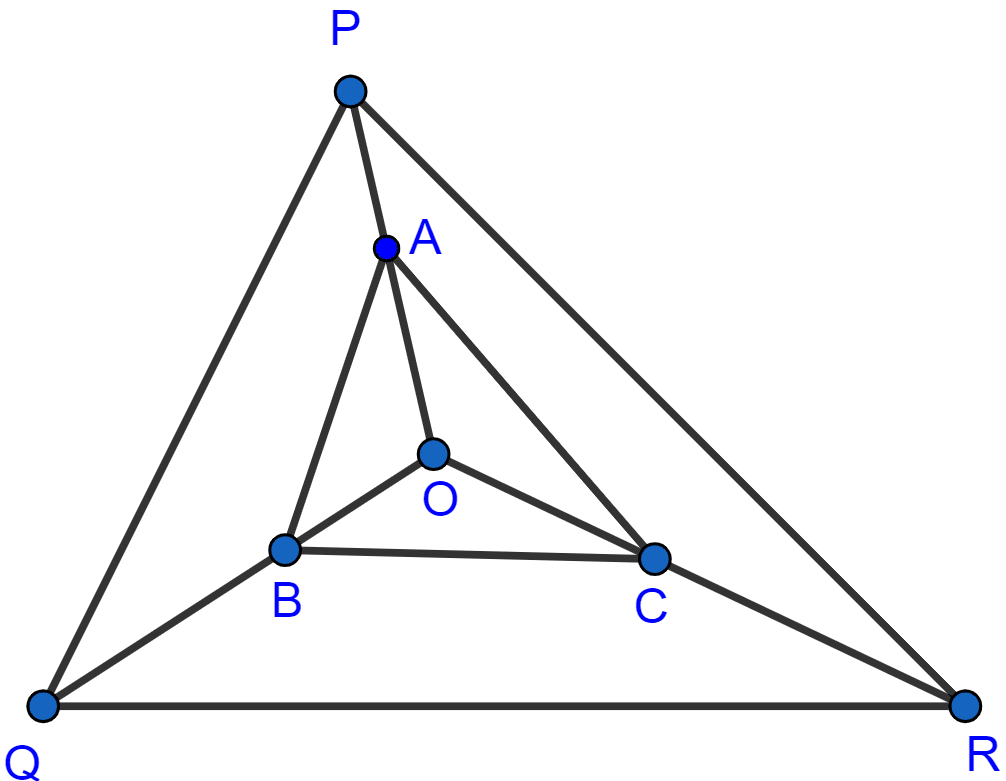
In the adjoining figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at O. Using Basic Proportionality theorem prove that