Mathematics
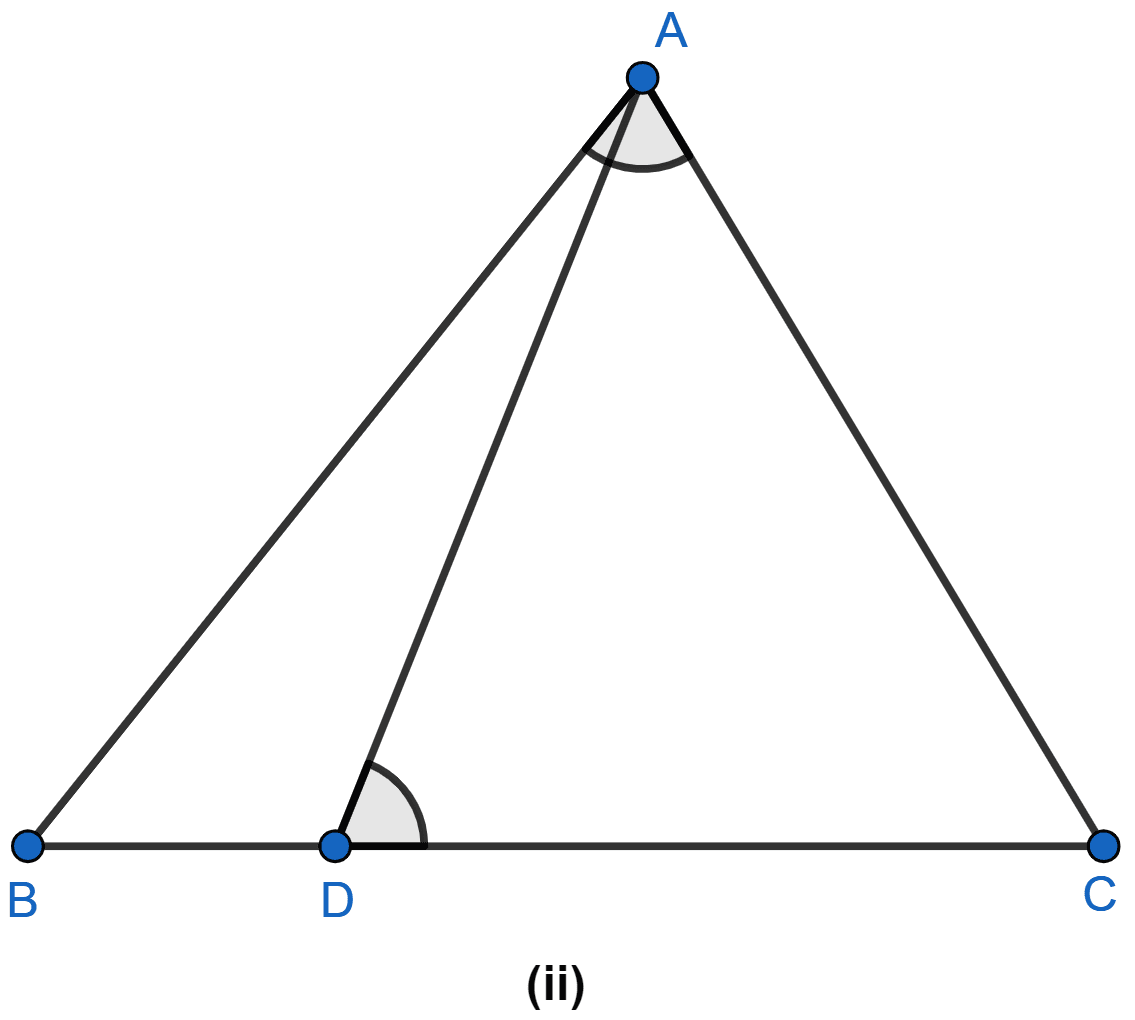
In the figure (ii) given below, ∠ADC = ∠BAC. Prove that CA2 = DC × BC.
Similarity
94 Likes
Answer
In △ABC and △ADC
∠C = ∠C (Common angle for both triangle)
∠BAC = ∠ADC (Given)
Then, by AA rule of similarity, △BAC ~ △ADC.
So,
Hence proved.
Answered By
55 Likes
Related Questions
In the figure (2) given below, CA ∥ BD, the lines AB and CD meet at O.
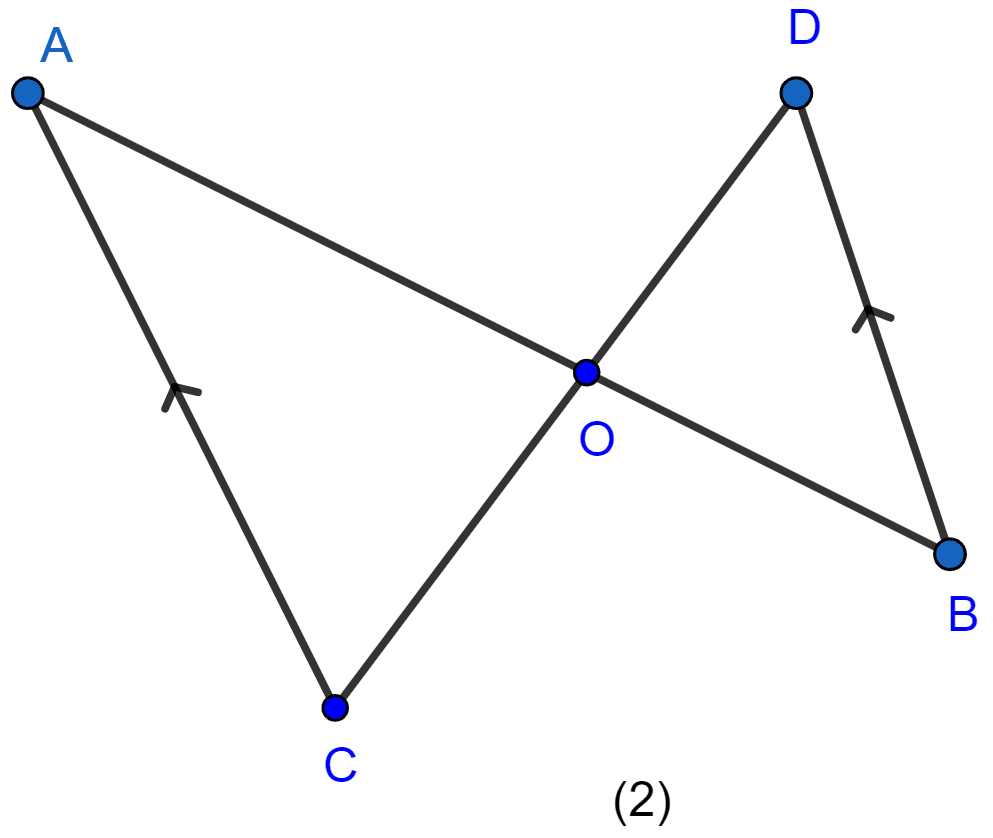
(i) Prove that △ACO ~ △BDO.
(ii) If BD = 2.4 cm, OD = 4 cm, OB = 3.2 cm and AC = 3.6 cm, calculate OA and OC.
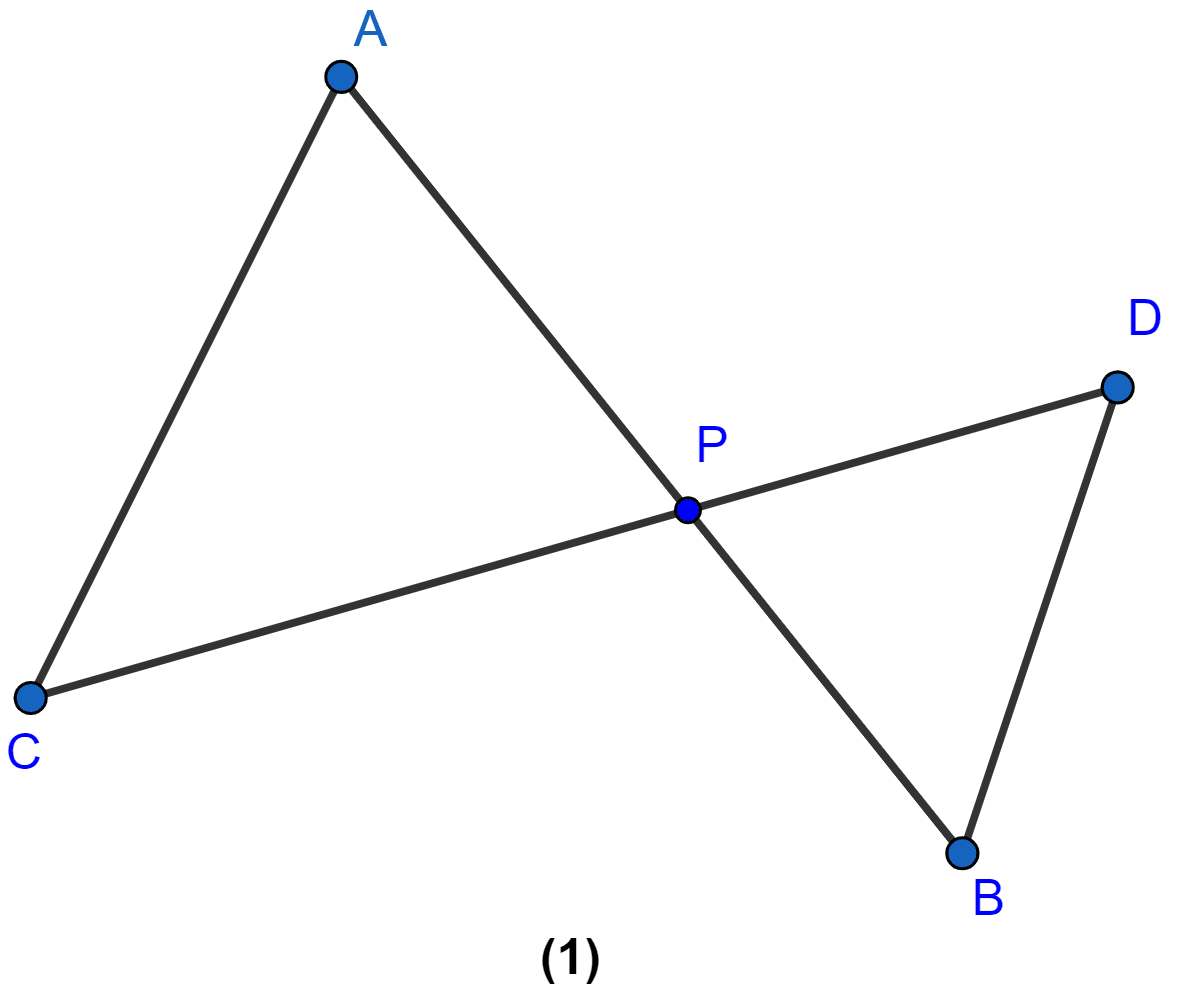
In the figure (1) given below, AP = 2PB and CP = 2PD.
(i) Prove that △ACP is similar to △BDP and AC ∥ BD.
(ii) If AC = 4.5 cm, calculate the length of BD.
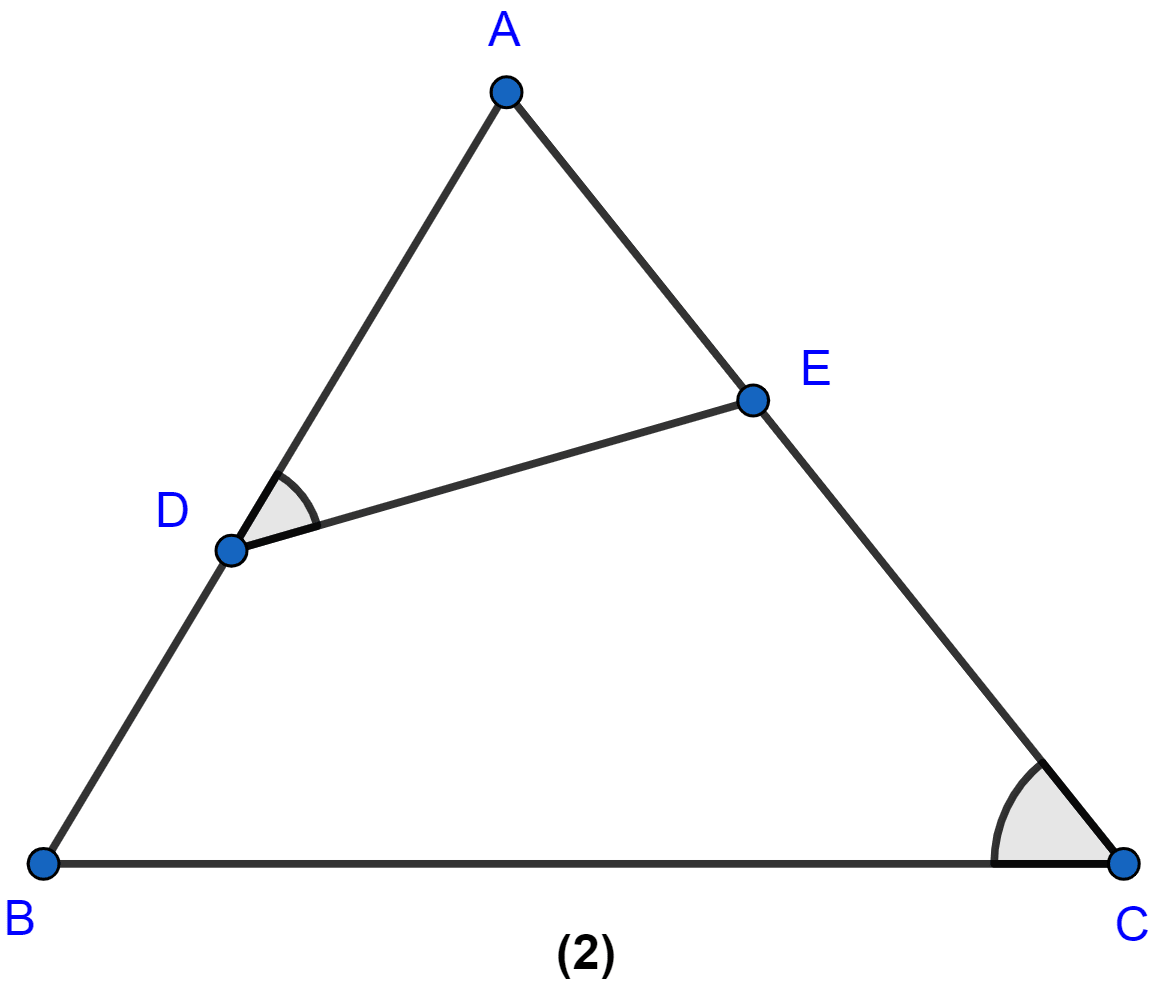
In the figure (2) given below, ∠ ADE = ∠ ACB.
(i) Prove that △s ABC and AED are similar.
(ii) If AE = 3 cm, BD = 1 cm and AB = 6 cm, calculate AC.
In the figure (i) given below, ∠P = ∠RTS. Prove that △RPQ ~ △RTS.
