Mathematics
In the figure (ii) given below, ∠ABC = ∠DAC and AB = 8 cm, AC = 4 cm, AD = 5 cm.
(i) Prove that △ACD is similar to △BCA.
(ii) Find BC and CD.
(iii) Find area of △ACD : area of △ABC.

Similarity
44 Likes
Answer
(i) Considering △ACD and △BCA.
∠C = ∠C (Common angles)
∠ABC = ∠DAC (Given)
Hence, by AA axiom △ACD ~ △BCA.
(ii) Since triangles are similar, hence the ratio of corresponding sides will be equal
Similarly,
Hence, the length of BC = 6.4 cm and CD = 2.5 cm.
(iii) We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
Hence, the ratio of area of △ACD : area of △ABC = 25 : 64.
Answered By
22 Likes
Related Questions
In the figure (ii) given below, AB || DC and AB = 2DC. If AD = 3 cm, BC = 4 cm and AD, BC produced meet at E, find
(i) ED
(ii) BE
(iii) area of △EDC : area of trapezium ABCD.

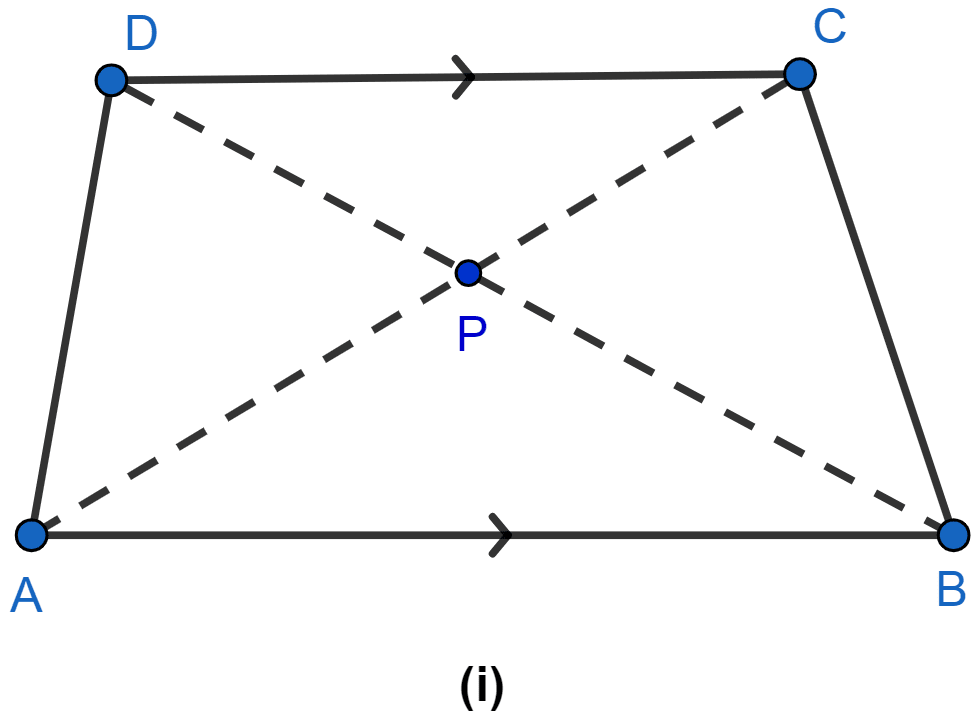
In the figure (i) given below, ABCD is a trapezium in which DC is parallel to AB. If AB = 9 cm, DC = 6 cm and BD = 12 cm, find
(i) BP
(ii) the ratio of areas of △APB and △DPC.
In the given figure,
∠ PQR = ∠ PST = 90°, PQ = 5 cm and PS = 2 cm.(i) Prove that △PQR ~ △PST.
(ii) Find area of △PQR : area of quadrilateral SRQT.

ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC.

(i) Prove that △ADE ~ △ACB.
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
(iii) Find, area of △ADE : area of quadrilateral BCED.