Mathematics
In the figure (ii) given below, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°. Find :
(i) ∠CAD
(ii) ∠CBD
(iii) ∠ADC

Answer
(i) ABCD is a cyclic quadrilateral.
Since exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
∴ ∠BCE = ∠DAB
⇒ ∠BCE = ∠CAD + ∠BAC
⇒ 80° = ∠CAD + 25°
⇒ ∠CAD = 80° - 25°
⇒ ∠CAD = 55°.
Hence, the value of ∠CAD = 55°.
(ii) From figure,
∠CBD = ∠CAD (∵ angles in same segment are equal.)
∠CBD = 55°.
Hence, the value of ∠CBD = 55°.
(iii) ∠BAC = ∠BDC (∵ angles in same segment are equal.)
∠BDC = 25°.
Now AB || DC and BD is the transversal
∠ABD = ∠BDC (∵ ∵ alternate angles are equal.)
⇒ ∠ABD = 25°
From figure,
∠ABC = ∠ABD + ∠CBD = 25° + 55° = 80°.
Since, sum of opposite angles of a cyclic quadrilateral is 180°.
⇒ ∠ABC + ∠ADC = 180°
⇒ 80° + ∠ADC = 180°
⇒ ∠ADC = 180° - 80°
⇒ ∠ADC = 100°.
Hence, the value of ∠ADC = 100°.
Related Questions
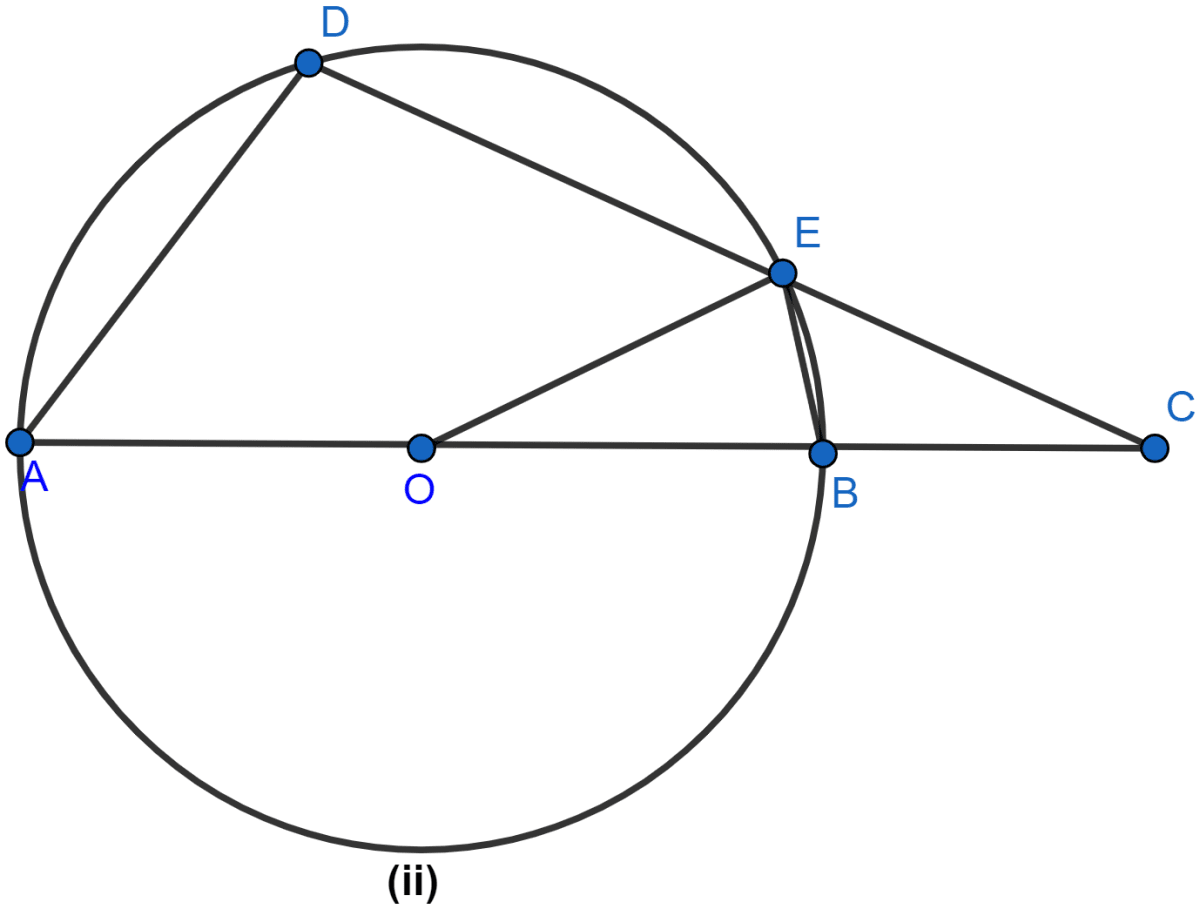
In the figure (ii) given below, O is the center of the circle. ∠AOE = 150°, ∠DAO = 51°. Calculate the sizes of ∠BEC and ∠EBC.
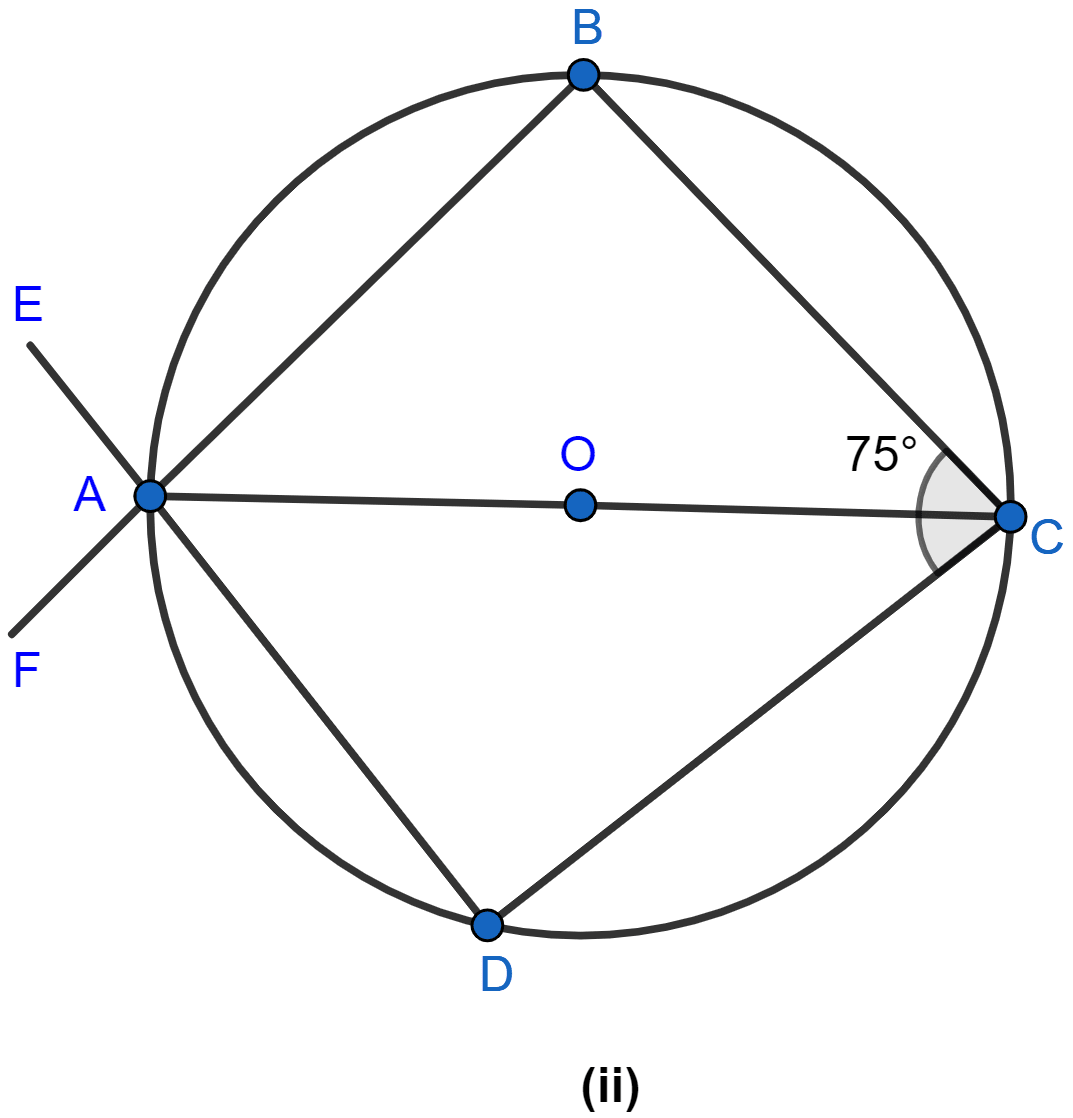
In the figure (ii) given below, AC is a diameter of the given circle and ∠BCD = 75°. Calculate the size of
(i) ∠ABC
(ii) ∠EAF
In the figure (i) given below, if ∠DBC = 58° and BD is a diameter of the circle, calculate
(i) ∠BDC
(ii) ∠BEC
(iii) ∠BAC

In the figure (i) given below, ABCD is a cyclic quadrilateral. If ∠ADC = 80° and ∠ACD = 52°, find the values of ∠ABC and ∠CBD.
