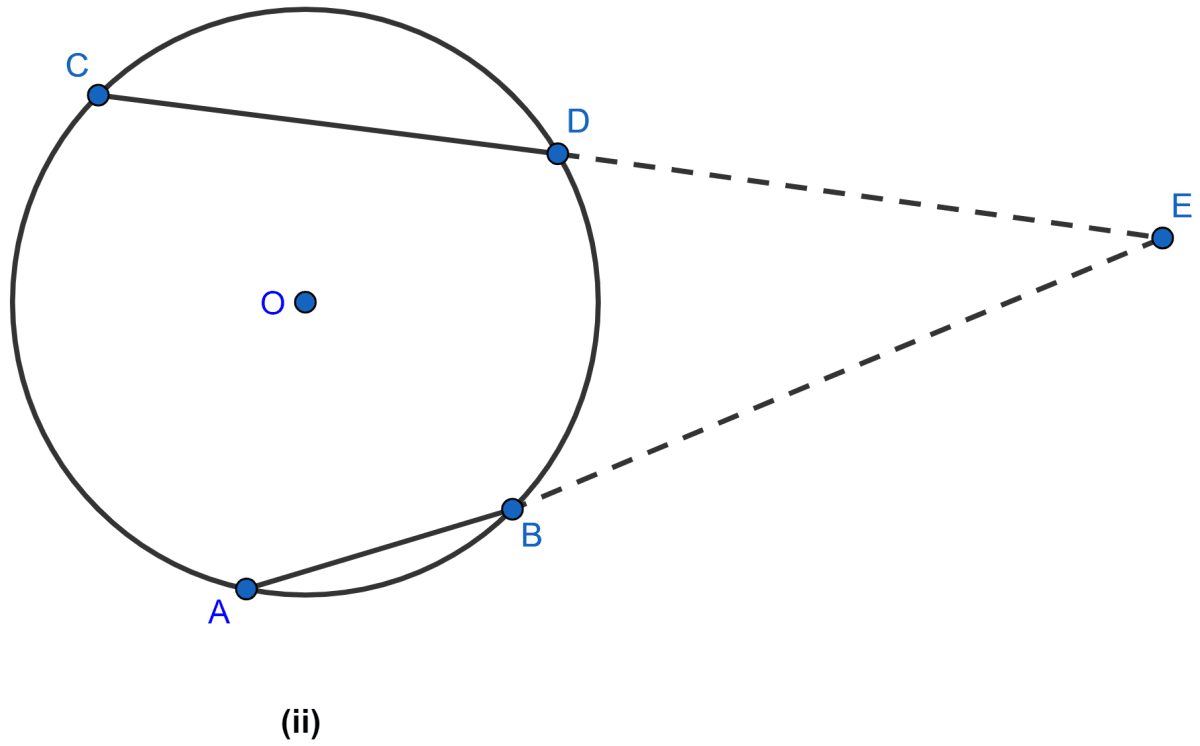
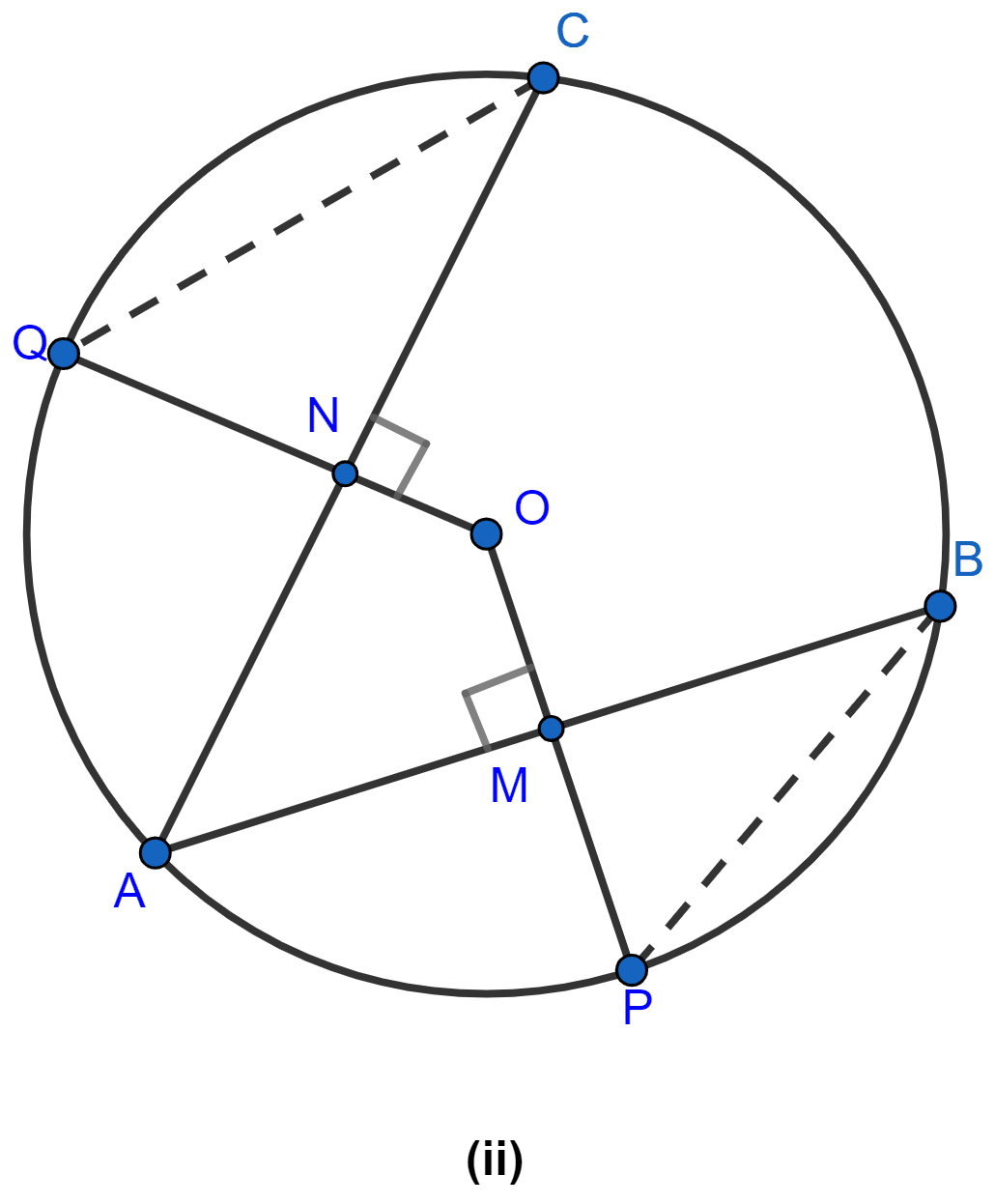
In the figure (ii) given below, O is the center of a circle. If AB and AC are chords of the circle such that AB = AC and OP ⊥ AB, OQ ⊥ AC, prove that PB = QC.

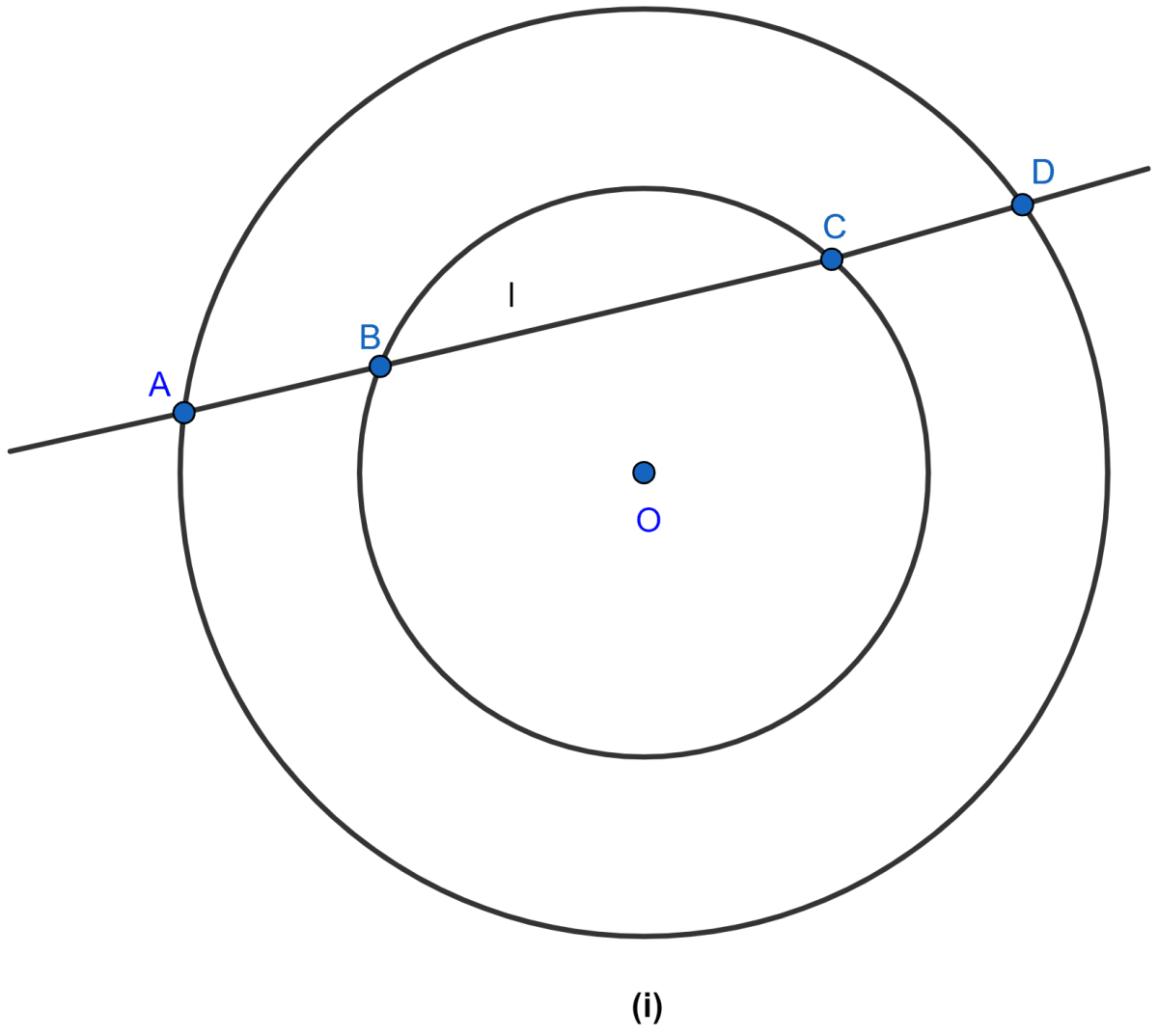
In the figure (i) given below, a line l intersects two concentric circles at the points A, B, C and D. Prove that AB = CD.

In the figure (ii) given below, chords AB and CD of a circle with centre O intersect at E. If OE bisects ∠AED, prove that AB = CD.

In the figure (i) given below, AD is a diameter of a circle with center O. If AB || CD, prove that AB = CD.