In the figure (ii) given below, AB and CD are equal chords of a circle with center O. If AB and CD meet at E (outside the circle) prove that

(i) AE = CE

(ii) BE = DE.

Draw ON ⊥ CD and OM ⊥ AB. Join OE.

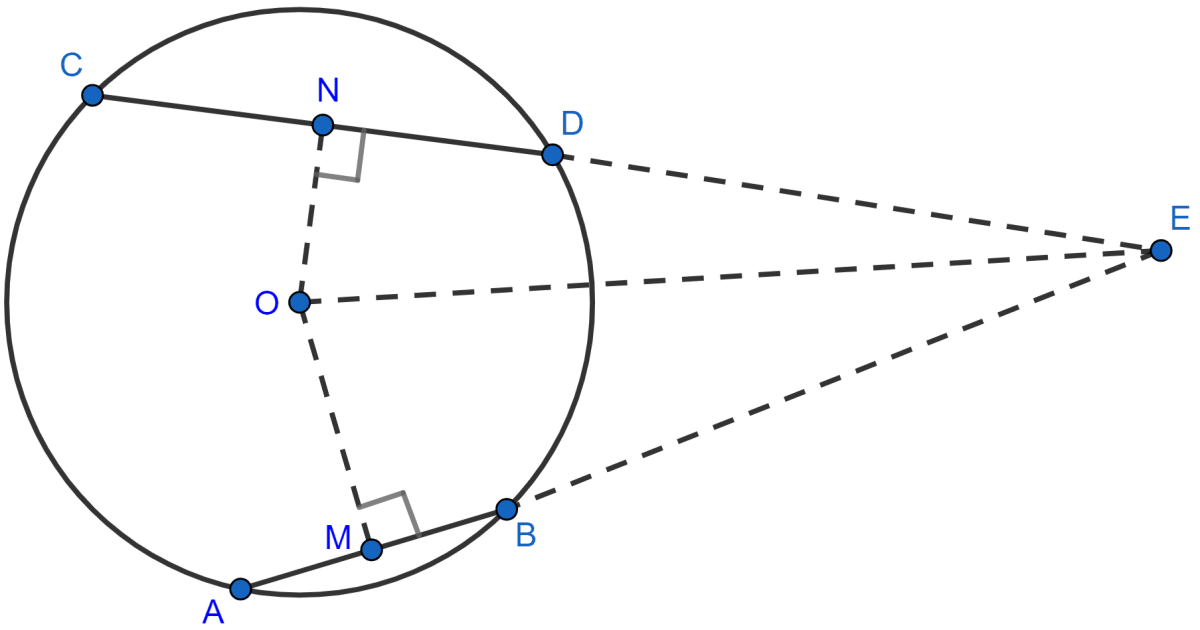
(i) Since, equal chords are equidistant from the center of the circle,

∴ ON = OM.

In △ONE and △OME,

ON = OM

∠ONE = ∠OME (Both equal to 90°)

OE = OE (Common side)

∴ △ONE ≅ △OME (By R.H.S. congruence rule).

∴ NE = ME = y (let) (By C.P.C.T.) ……..(1)

Let AB = CD = x.

Since, the perpendicular to a chord from the centre of the circle bisects the chord,

∴ CN = ND = $\dfrac{CD}{2} = \dfrac{x}{2}$ and

AM = MB = $\dfrac{AB}{2} = \dfrac{x}{2}$.

From figure,

AE = AM + ME = $\dfrac{x}{2} + y$

CE = CN + NE = $\dfrac{x}{2} + y$

Hence, proved that AE = CE.

(ii) From figure,

BE = ME - MB = $y - \dfrac{x}{2}$

DE = NE - ND = $y - \dfrac{x}{2}$

Hence, proved that BE = DE.