Mathematics
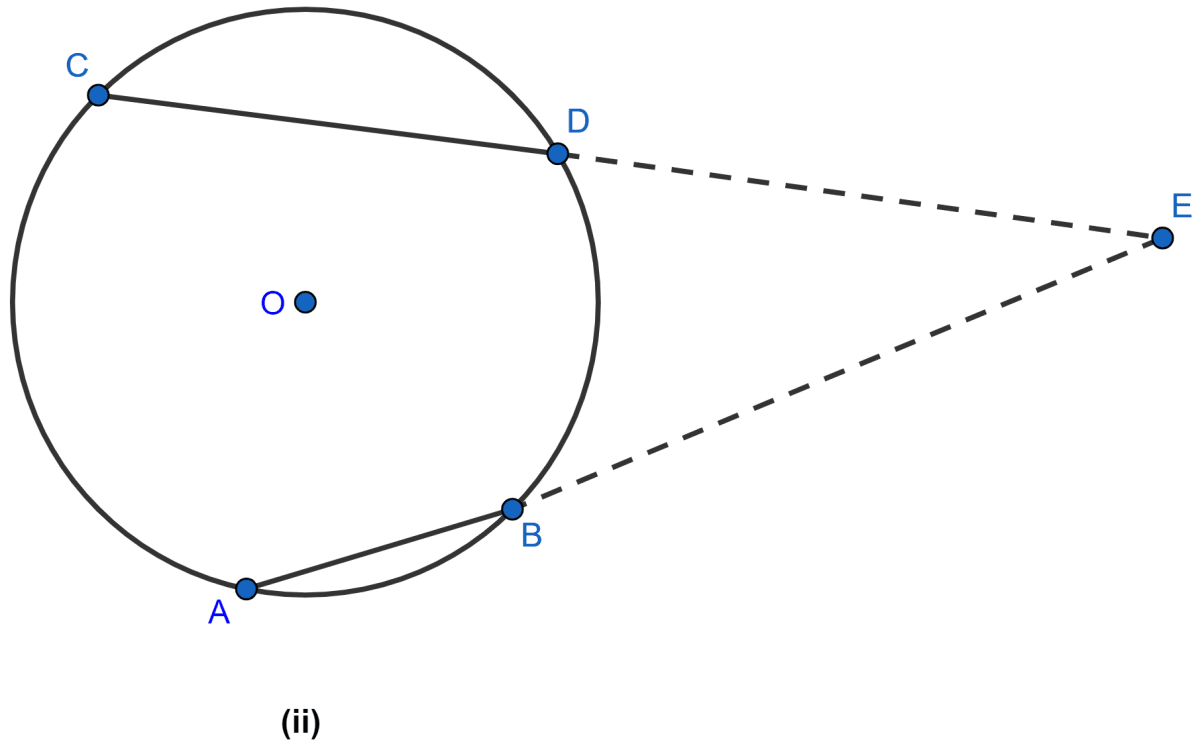
In the figure (ii) given below, AB and CD are equal chords of a circle with center O. If AB and CD meet at E (outside the circle) prove that
(i) AE = CE
(ii) BE = DE.
Related Questions
In the figure (ii) given below, chords AB and CD of a circle with centre O intersect at E. If OE bisects ∠AED, prove that AB = CD.

In the figure (i) given below, AD is a diameter of a circle with center O. If AB || CD, prove that AB = CD.

If arcs APB and CQD of a circle are congruent, then find the ratio of AB : CD.
A and B are points on a circle with center O. C is a point on the circle such that OC bisects ∠AOB, prove that OC bisects the arc AB.