Mathematics
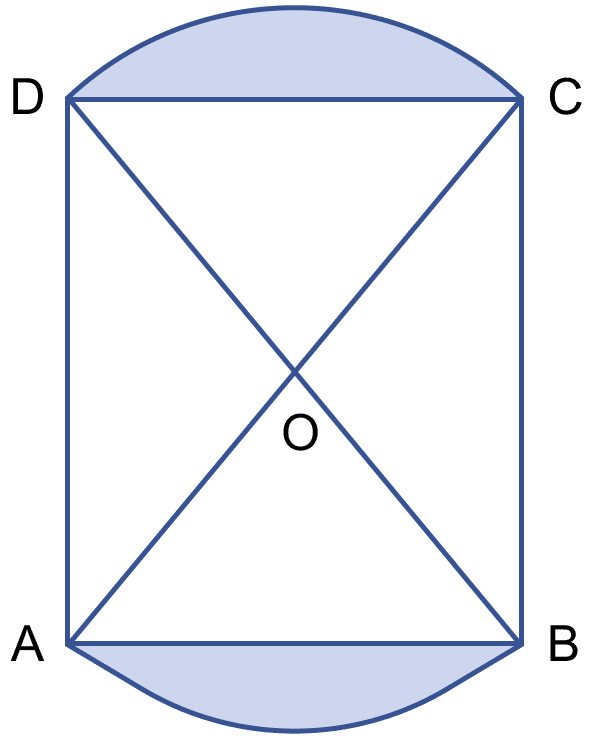
In the figure (i) given below, two circular flower beds have been shown on the two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
Mensuration
51 Likes
Answer
Area of lawn ABCD = (side)2
= (56)2 = 3136 m2.
In square,
Length of diagonal (AC) = side = m.
Since, diagonals of square are equal and bisect each other,
∴ AO = OC = OD = OB.
Radius of quadrant ODC = Radius of quadrant OAB = m.
Area of quadrant ODC = Area of quadrant OAB =
Since, diagonals of square divide it into four equal triangles.
Area of △ODC = Area of △OAB = = 784 m2.
From figure,
Area of flower bed = Area of quadrant ODC - Area of △ODC
= 1232 - 784 = 448 m2.
Since there are two flower beds so area = 2 × 448 = 896 m2.
Area of lawn and flower beds = 3136 + 896 = 4032 m2.
Hence, sum of the areas of the lawn and the flower beds = 4032 m2.
Answered By
32 Likes
Related Questions
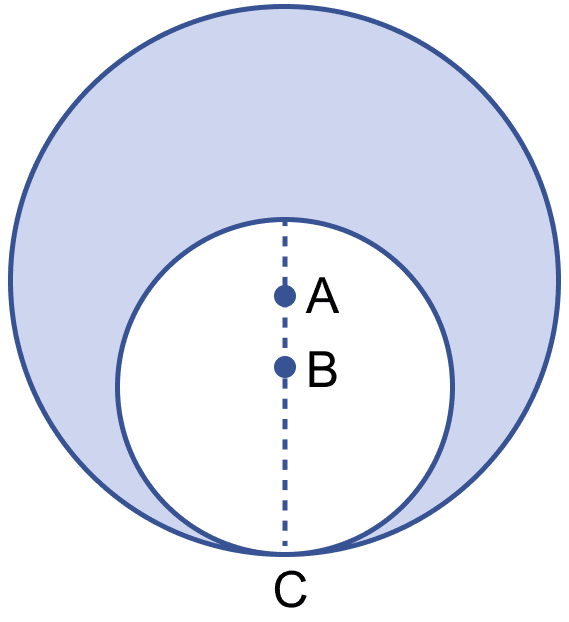
In the figure (i) given below, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.
The quadrants shown in the figure (ii) given below are each of radius 7 cm. Calculate the area of the shaded portion.

In the figure (ii) given below, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (π = 3.14)

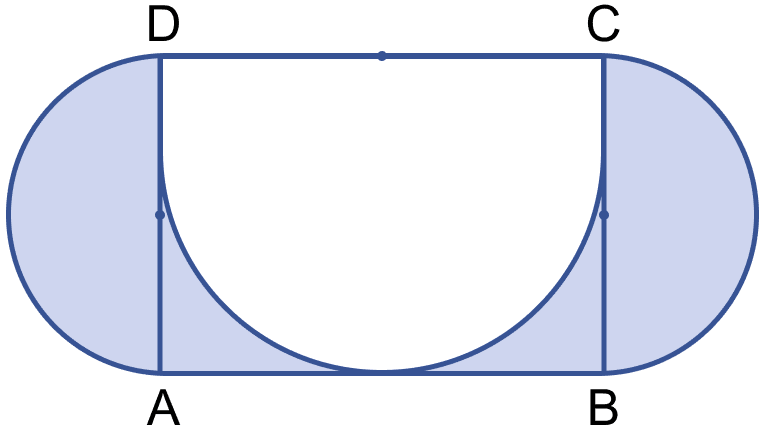
In the figure (i) given below, ABCD is a rectangle, AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semicircles are drawn as shown in the figure. Find the area of the shaded portion.