Mathematics
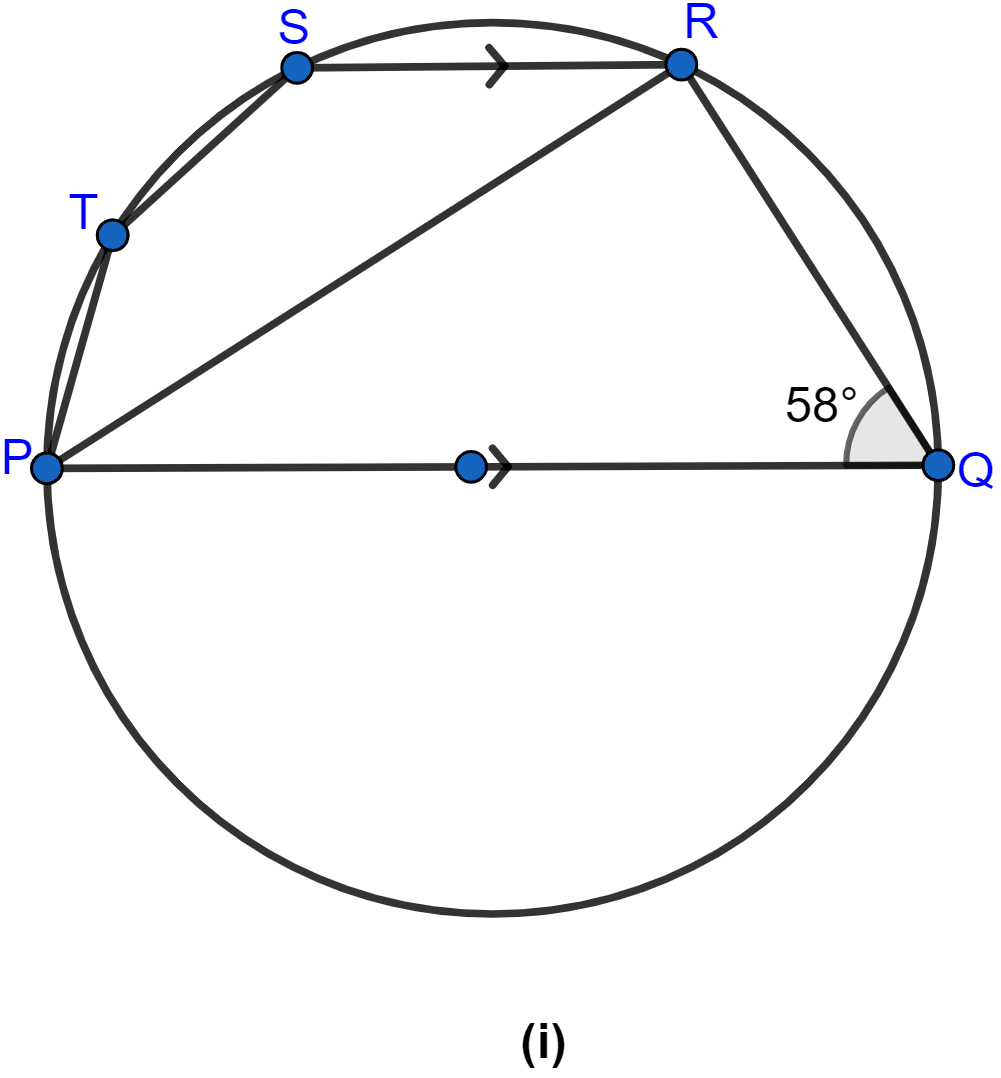
In the figure (i) given below, PQ is a diameter. Chord SR is parallel to PQ. Given ∠PQR = 58°, calculate
(i) ∠RPQ
(ii) ∠STP
(T is a point on the minor arc SP)
Answer
(i) From figure,
∠PRQ = 90° (∵ angle in semicircle is equal to 90°.)
Since sum of angles in triangle is 180°.
⇒ ∠PRQ + ∠RQP + ∠RPQ = 180°
⇒ 90° + 58° + ∠RPQ = 180°
⇒ ∠RPQ + 148° = 180°
⇒ ∠RPQ = 180° - 148
⇒ ∠RPQ = 32°.
Hence, the value of ∠RPQ = 32°.
(ii) From figure,
∠SRP = ∠RPQ = 32° (∵ alternate angles are equal.)
Since, PTSR is a cyclic quadrilateral so sum of its opposite angles is equal to 180°.
⇒ ∠SRP + ∠STP = 180°
⇒ 32° + ∠STP = 180°
⇒ ∠STP = 180° - 32°
⇒ ∠STP = 148°.
Hence, the value of ∠STP = 148°.
Related Questions
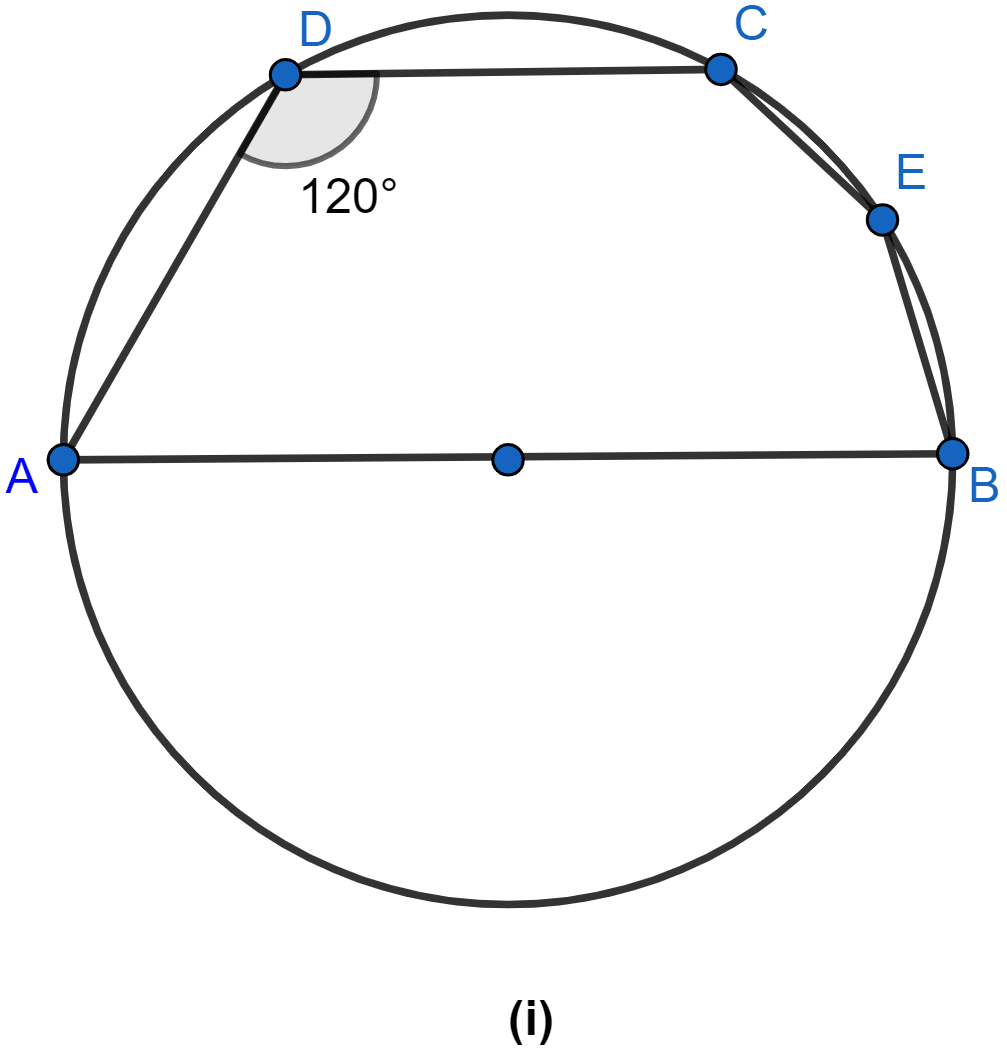
In the figure (i) given below, AB is a diameter of the circle. If ∠ADC = 120°, find ∠CAB.
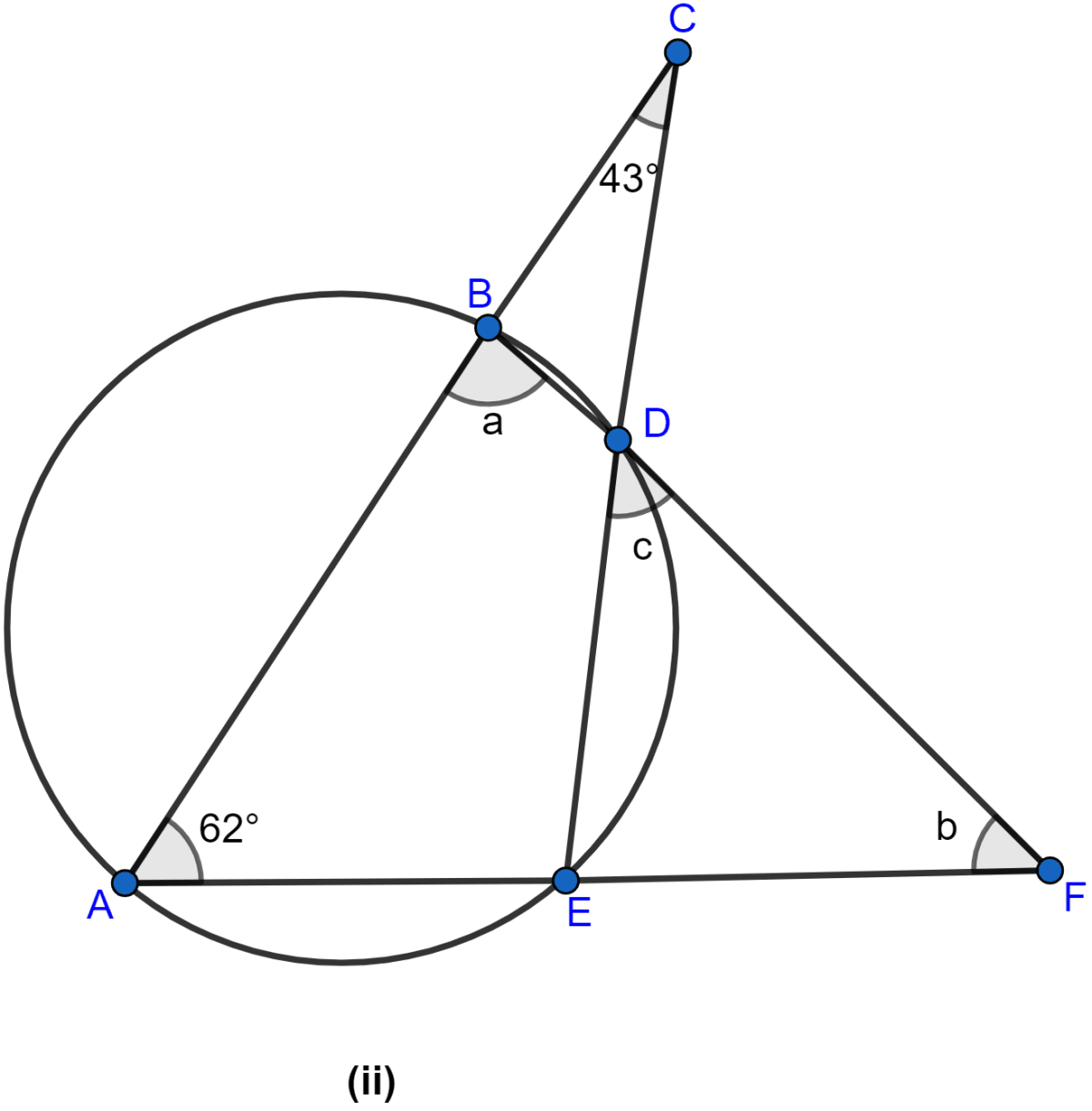
In the figure (ii) given below, if ∠ACE = 43° and ∠CAF = 62°, find the values of a, b and c.
In the figure (ii) given below, two circles intersect at points P and Q. If ∠A = 80° and ∠D = 84°, calculate
(i) ∠QBC
(ii) ∠BCP

In the figure (i) given below, O is the center of the circle. If ∠BAD = 30°, find the values of p, q and r.
