Mathematics
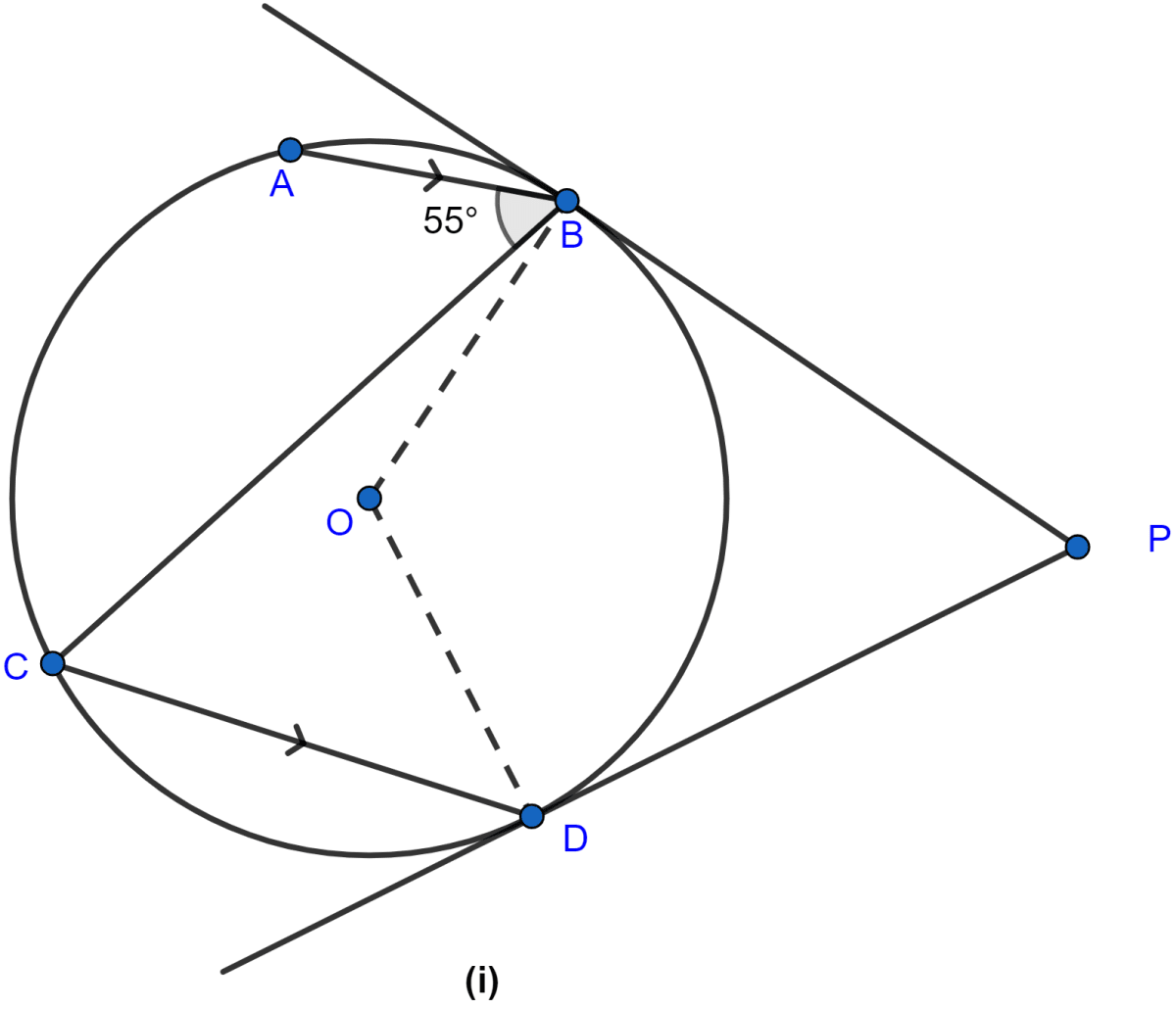
In the figure (i) given below, O is the centre of the circle. The tangents at B and D meet at P. If AB is parallel to CD and ∠ABC = 55°, find
(i) ∠BOD
(ii) ∠BPD.
Circles
25 Likes
Answer
(i) From figure,
∠BCD = ∠ABC (∵ alternate angles are equal)
∠BCD = 55°.
Arc BD subtends ∠BOD at the centre and ∠BCD at the remaining part of the circle.
∴ ∠BOD = 2∠BCD (∵ angle subtended at centre by an arc is double the angle subtended at remaining point of circle.)
∠BOD = 2 × 55° = 110°.
Hence, the value of ∠BOD = 110°
(ii) OB and OD are radius and, BP and DP are tangents to the circle.
∴ OB ⊥ BP and OD ⊥ DP.
In quadrilateral OBPD, sum of angles = 360°
∠BOD + ∠ODP + ∠OBP + ∠BPD = 360°
110° + 90° + 90° + ∠BPD = 360°
290° + ∠BPD = 360°
∠BPD = 360° - 290°
∠BPD = 70°.
Hence, the value of ∠BPD = 70°.
Answered By
15 Likes
Related Questions
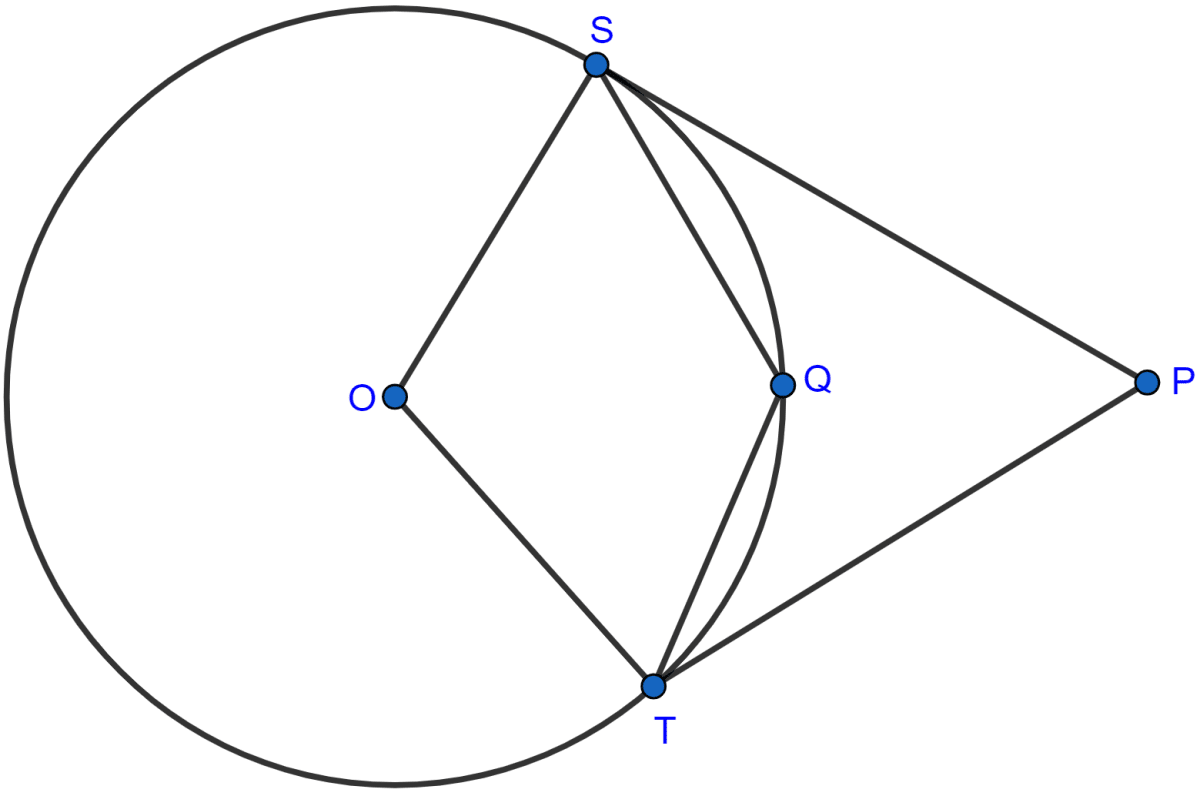
In the figure (ii) given below, O is the centre of the circle. PS and PT are tangents and ∠SPT = 84°. Calculate the sizes of the angles TOS and TQS.
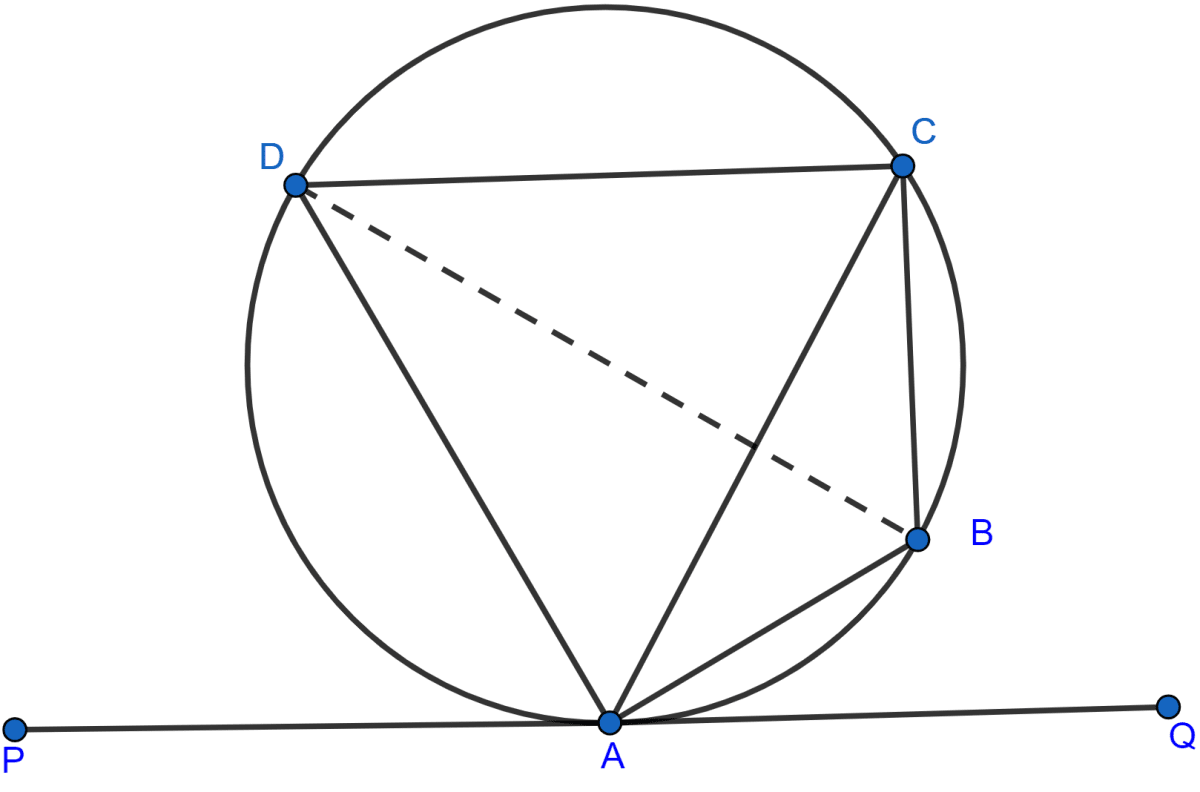
In the adjoining figure, O is the centre of the circle. Tangents to the circle at A and B meet at C. If ∠ACO = 30°, find
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB

In the figure (ii) given below, O is the centre of the circle. AB is a diameter, TPT' is a tangent to the circle at P. If ∠BPT' = 30°, calculate
(i) ∠APT
(ii) ∠BOP

In the adjoining figure, ABCD is a cyclic quadrilateral. The line PQ is the tangent to the circle at A. If ∠CAQ : ∠CAP = 1 : 2, AB bisects ∠CAQ and AD bisects ∠CAP, then find the measures of the angles of the cyclic quadrilateral. Also prove that BD is a diameter of the circle.