Mathematics
In the figure (i) given below, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
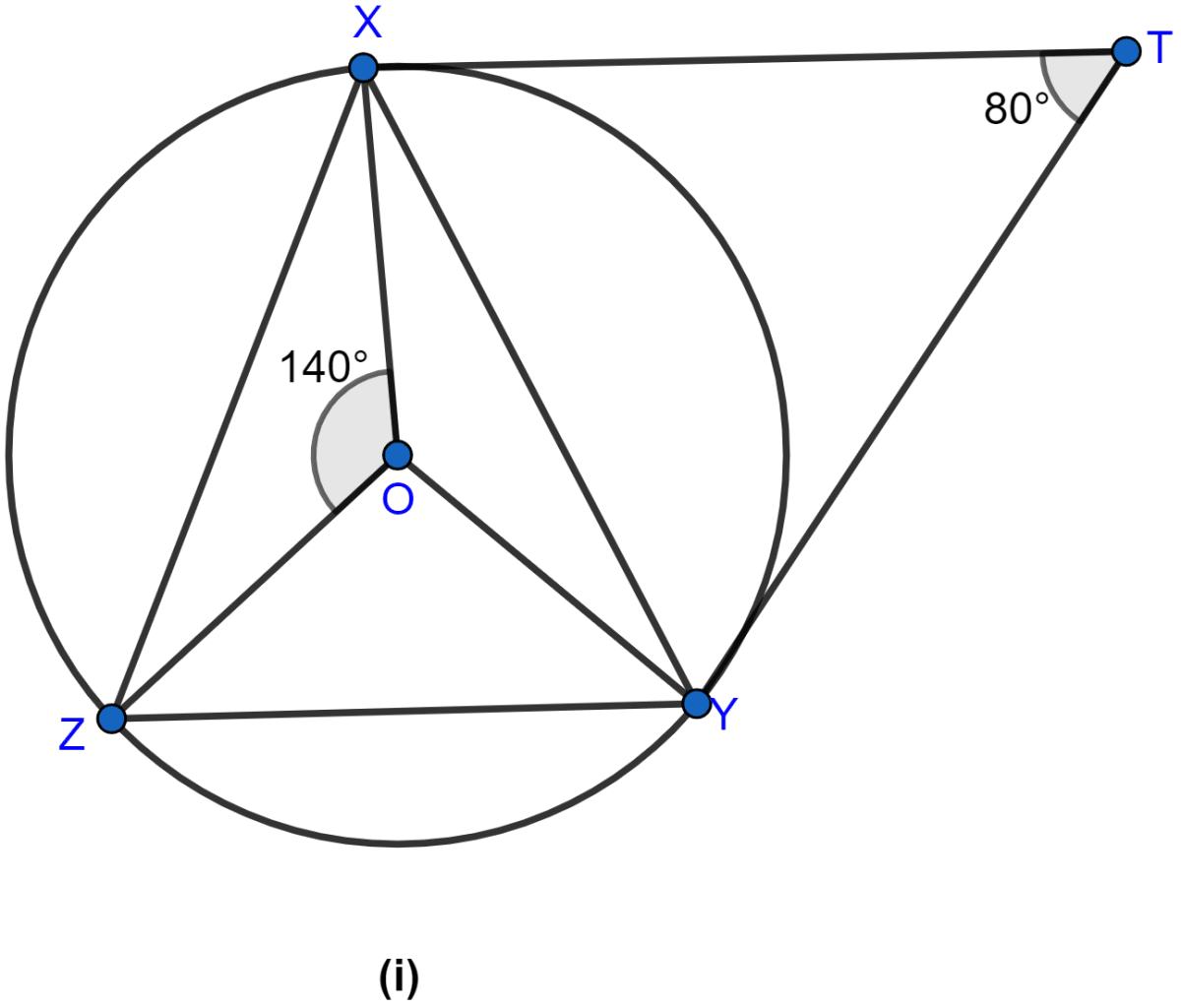
Answer
From figure,
XT = YT (∵ tangents from an external point to a circle are of equal length.)
So, △XTY is an isosceles triangle with
∠YXT = ∠XYT = a.
Since sum of angles in a triangle = 180°.
In △XTY,
⇒ ∠YXT + ∠XYT + ∠XTY = 180°
⇒ a + a + 80° = 180°
⇒ 2a + 80° = 180°
⇒ 2a = 180° - 80°
⇒ 2a = 100°
⇒ a = 50°.
From figure,
OX = OZ = radius of the circle
So, △OXZ is an isosceles triangle with
∠OXZ = ∠OZX = b.
Since sum of angles in a triangle = 180°.
In △OXZ,
⇒ ∠OXZ + ∠OZX + ∠XOZ = 180°
⇒ b + b + 140° = 180°
⇒ 2b + 140° = 180°
⇒ 2b = 180° - 140°
⇒ 2b = 40°
⇒ b = 20°.
From figure,
OX ⊥ XT (∵ tangent at a point and radius through the point are perpendicular to each other.)
∴ ∠OXT = 90°
∠OXY + ∠YXT = 90°
∠OXY + 50° = 90°
∠OXY = 90° - 50°
∠OXY = 40°.
From figure,
∠ZXY = ∠OXZ + ∠OXY = 20° + 40° = 60°.
Hence, the value of ∠ZXY = 60°.
Related Questions
In the figure (ii) given below, AP and BP are tangents to the circle with centre O. Given ∠APB = 60°, calculate :
(i) ∠AOB
(ii) ∠OAB
(iii) ∠ACB

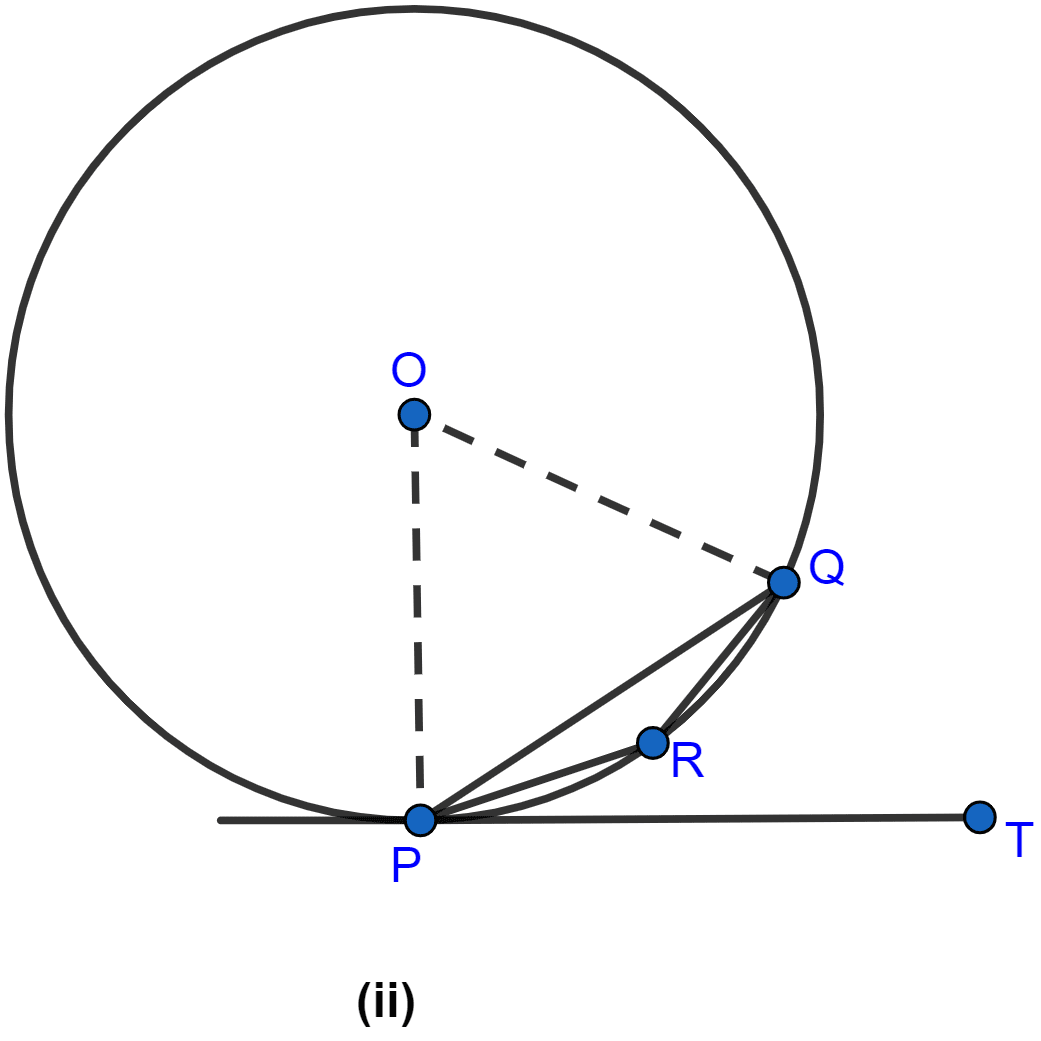
In the figure (ii) given below, O is the center of the circle and PT is the tangent to the circle at P. Given ∠QPT = 30°, calculate
(i) ∠PRQ
(ii) ∠POQ.
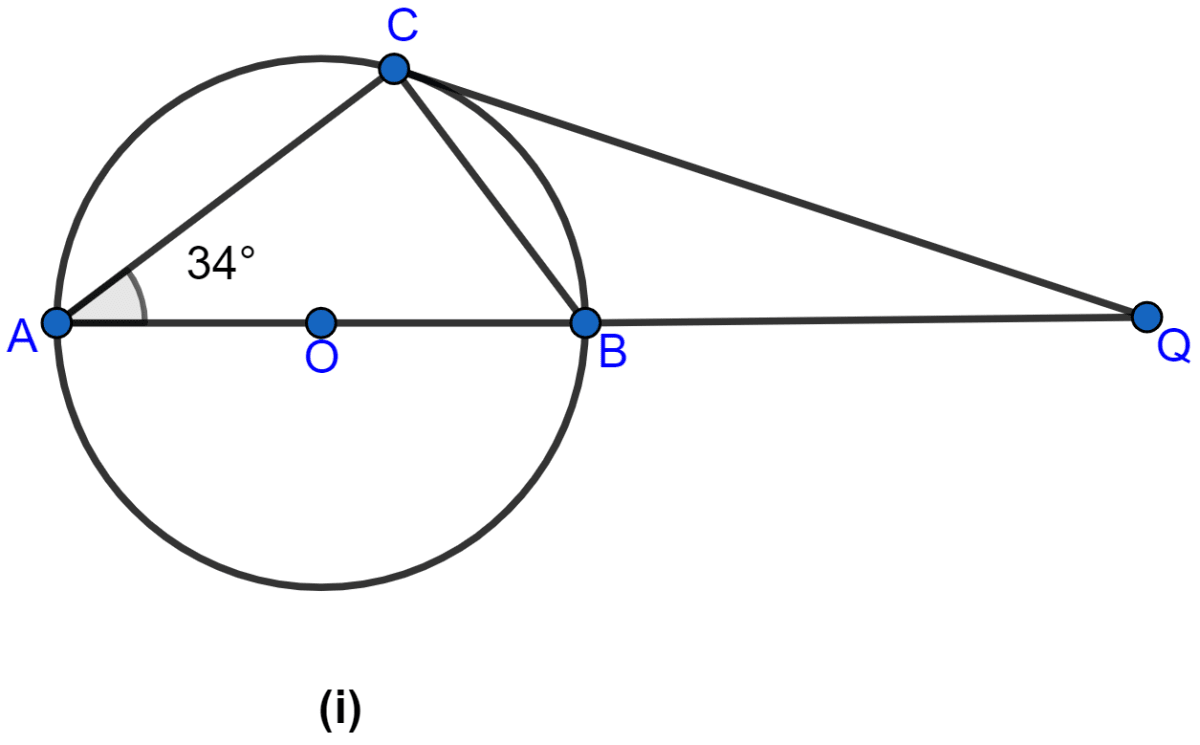
In the figure (i) given below, AB is a diameter. The tangent at C meets AB produced at Q, ∠CAB = 34°. Find :
(i) ∠CBA
(ii) ∠CQA
Two chords AB, CD of a circle intersect internally at a point P. If
(i) AP = 6 cm, PB = 4 cm and PD = 3 cm, find PC.
(ii) AB = 12 cm, AP = 2 cm, PC = 5 cm, find PD.
(iii) AP = 5 cm, PB = 6 cm and CD = 13 cm, find CP.