Mathematics
In the figure (i) given below, O is the center of the circle. If ∠BAD = 30°, find the values of p, q and r.

Answer
From figure,
ABCD is a cyclic quadrilateral as all vertices lie on the circumference of the circle.
Sum of opposite angles of cyclic quadrilateral = 180°
⇒ ∠A + ∠C = 180°
⇒ 30° + p = 180°
⇒ p = 180° - 30°
⇒ p = 150°.
∠BAD = ∠BED (∵ angles in same segment are equal.)
⇒ r = 30°.
Arc BD subtends ∠BAD at point A and ∠BOD at center.
∠BOD = 2∠BAD (∵ angle subtended by an arc at center is double the angle subtended at any other point of the circle.)
q = 2 × 30°
q = 60°.
Hence, the value of p = 150°, q = 60° and r = 30°.
Related Questions
In the figure (i) given below, ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. Given that ∠BEF = 80°, find ∠ABC.

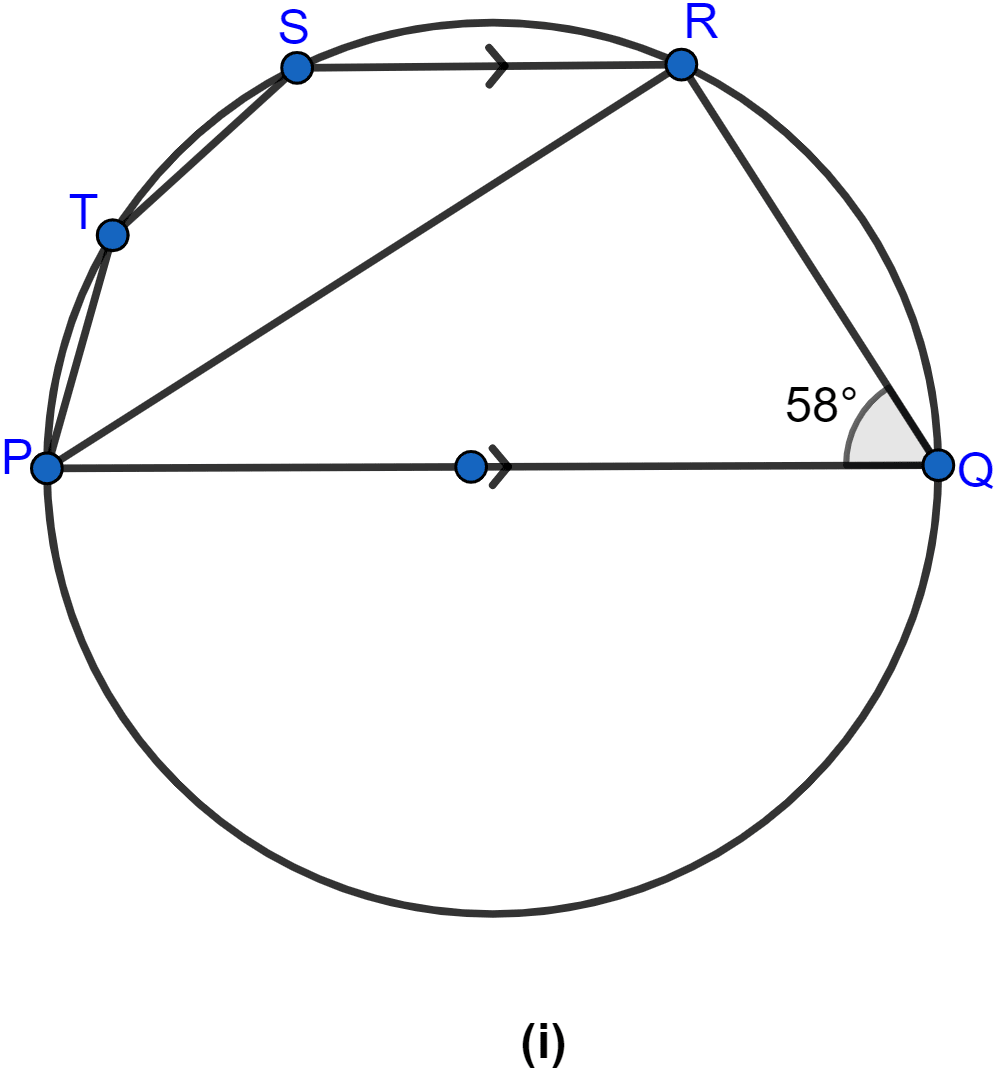
In the figure (i) given below, PQ is a diameter. Chord SR is parallel to PQ. Given ∠PQR = 58°, calculate
(i) ∠RPQ
(ii) ∠STP
(T is a point on the minor arc SP)
In the figure (ii) given below, ABCD is a cyclic trapezium in which AD is parallel to BC and ∠B = 70°, find
(i) ∠BAD
(ii) ∠BCD

In the figure (ii) given below, two circles intersect at points P and Q. If ∠A = 80° and ∠D = 84°, calculate
(i) ∠QBC
(ii) ∠BCP
