Mathematics
In the figure (i) given below, ABCD is a rectangle. AB = 14 cm, BC = 7 cm. From the rectangle, a quarter circle BFEC and a semicircle DGE are removed. Calculate the area of the remaining piece of the rectangle.

Mensuration
17 Likes
Answer
Area of rectangle = AB × BC = 14 × 7 = 98 cm2.
Since, ABCD is a rectangle.
∴ CD = AB = 14 cm.
BFEC is a quadrant of radius, BC = r1 = 7 cm.
∴ CE = 7 cm.
From figure,
DE = CD - CE = 14 - 7 = 7 cm.
From figure,
DE is the diameter of semi-circle DGE.
So, radius (r) = = 3.5 cm.
Area of semi-circle =
Area of quadrant BFEC =
Area of remaining piece of rectangle = Area of rectangle - Area of semicircle DGE - Area of quadrant BFEC
= 98 - 19.25 - 38.5
= 40.25 cm2.
Hence, area of remaining piece of rectangle = 40.25 cm2.
Answered By
11 Likes
Related Questions
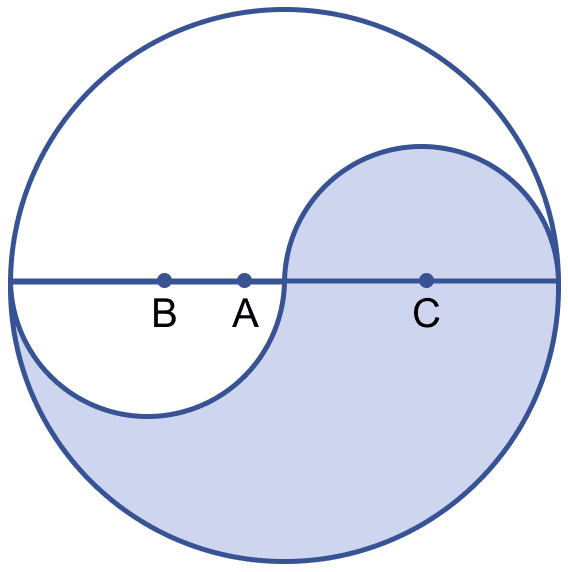
In the figure (i) given below, the points A, B and C are centres of arcs of circles of radii 5 cm, 3 cm and 2 cm respectively. Find the perimeter and the area of the shaded region. (Take π = 3.14)
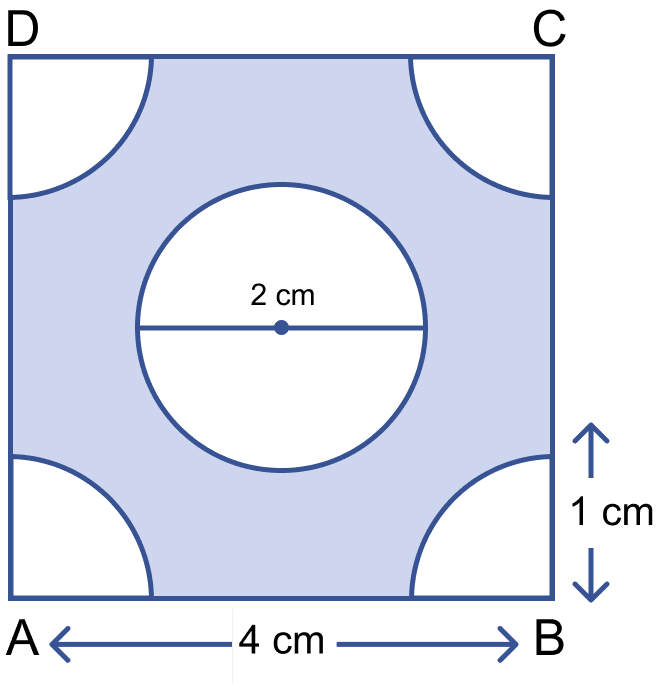
In the figure (ii) given below, ABCD is a square of side 4 cm. At each corner of the square a quarter circle of radius 1 cm, and at the centre a circle of diameter 2 cm are drawn. Find the area of the shaded region. Take π = 3.14.
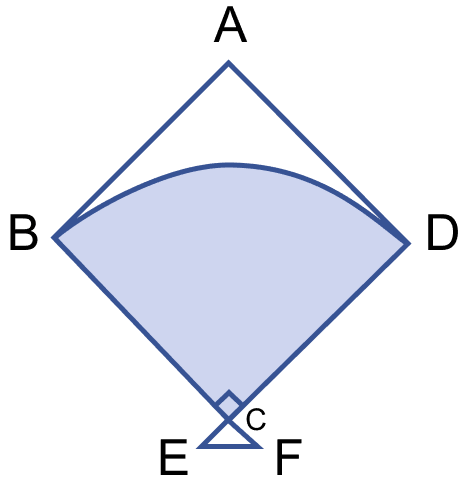
The figure (ii) given below shows a kite, in which BCD is in the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and △CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
In the figure (i) given below, the boundary of the shaded region in the given diagram consists of four semicircular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, calculate
(i) the length of the boundary.
(ii) the area of the shaded region.
