Mathematics
In the figure (i) given below, ABC is an equilateral triangle with each side of length 10 cm. In △BCD, ∠D = 90° and CD = 6 cm. Find the area of the shaded region. Give your answer correct to one decimal place.

Mensuration
38 Likes
Answer
Given,
ABC is an equilateral triangle of side = 10 cm
We know that,
Area of equilateral triangle ABC =
Substituting the values we get,
In right angled triangle BCD,
⇒ BC2 = BD2 + CD2
⇒ 102 = BD2 + 62
⇒ BD2 = 100 - 36
⇒ BD2 = 64
⇒ BD = 8 cm.
We know that,
Area of right angled triangle = × base × height.
Area of △BCD = = 24 cm2
From figure,
Area of shaded portion = Area of triangle ABC - Area of triangle BCD
Substituting the values we get,
Area of shaded portion = 43.3 - 24 = 19.3 cm2.
Hence, area of shaded region = 19.3 cm2.
Answered By
22 Likes
Related Questions
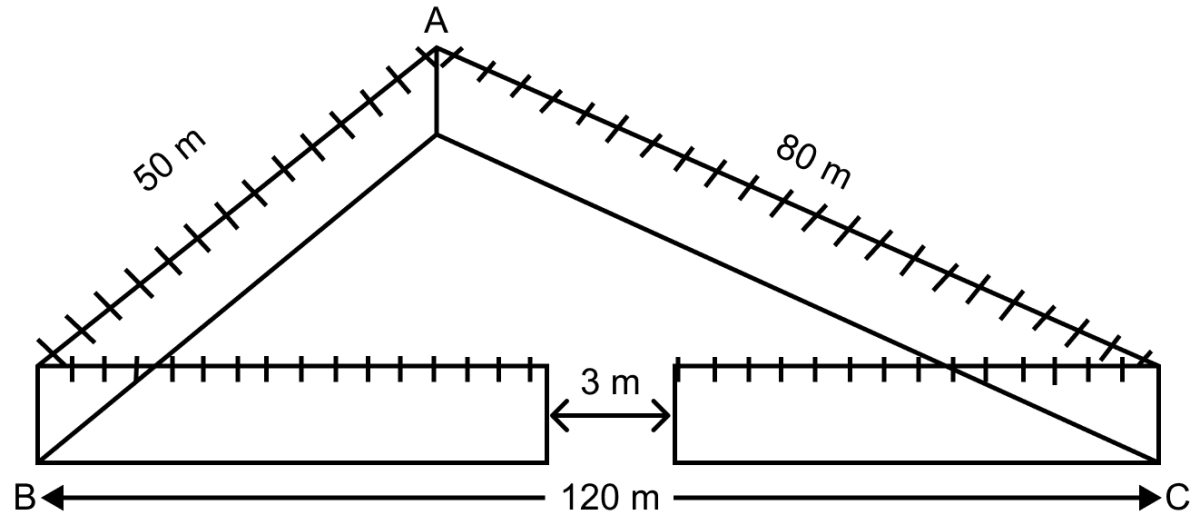
A triangular park ABC has sides 120 m, 80 m and 50 m (as shown in the adjoining figure). A gardner Dhania has to put a fence around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of ₹ 20 per metre leaving a space 3 m wide for a gate on one side.
An umbrella is made by stitching 10 triangular pieces of cloth of two different colors (shown in the adjoining figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

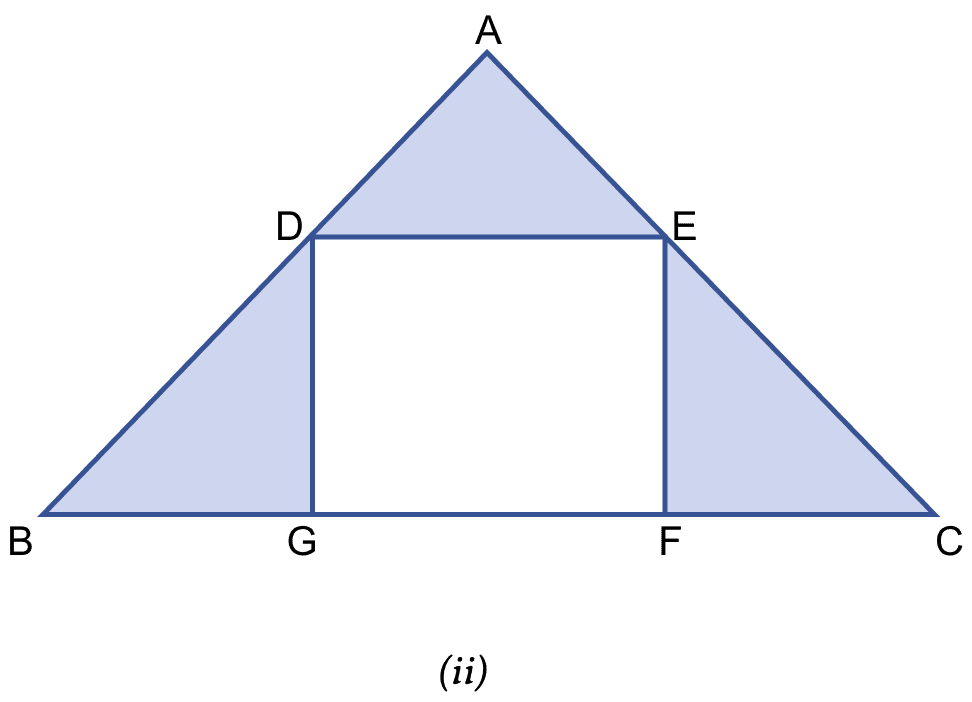
In the figure (ii) given, ABC is an isosceles right-angled triangle and DEFG is a rectangle. If AD = AE = 3 cm and DB = EC = 4 cm, find the area of the shaded region.
Find the area of quadrilateral whose one diagonal is 20 cm long and the perpendiculars to this diagonal from other vertices are of length 9 cm and 15 cm.