Mathematics
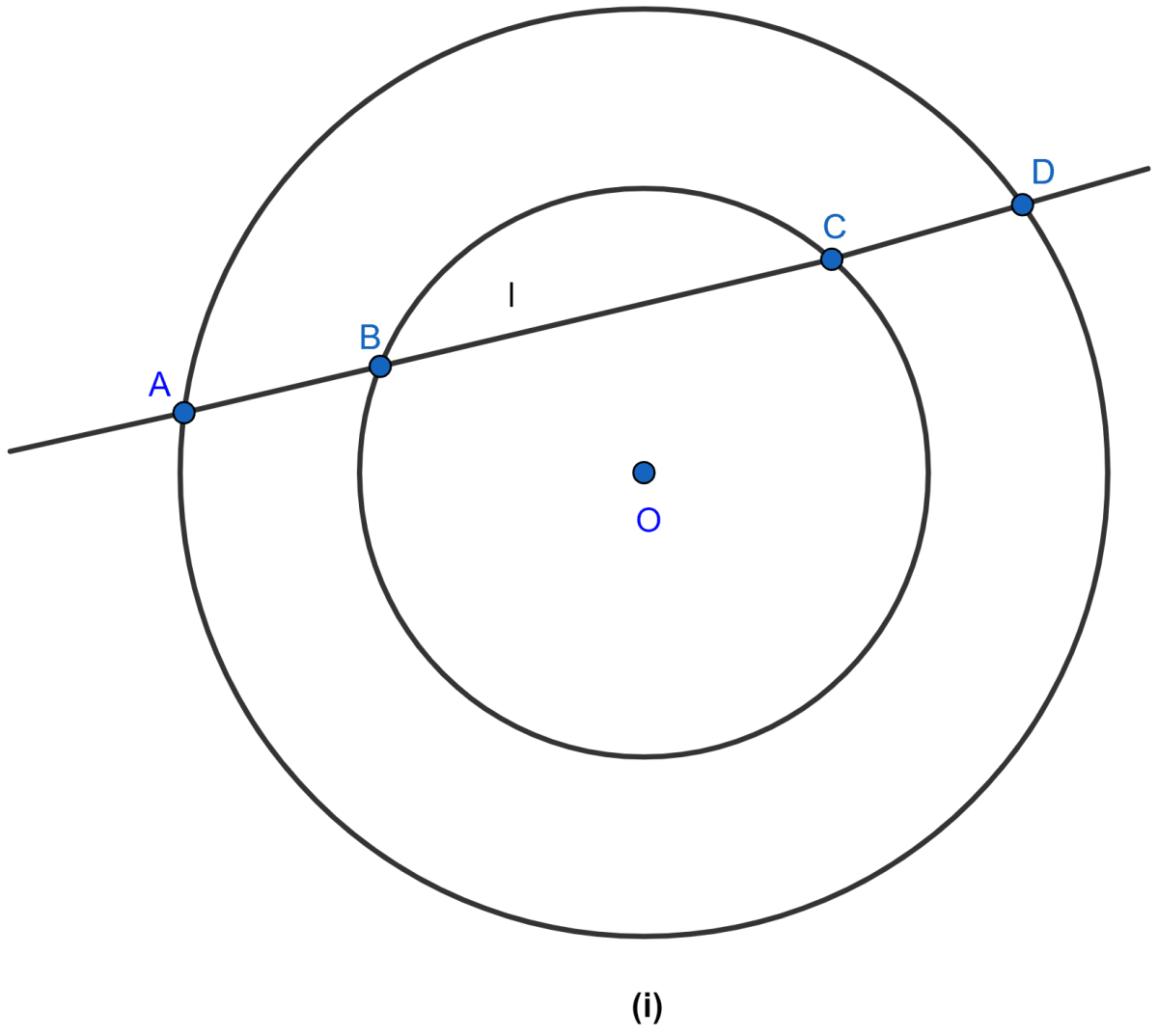
In the figure (i) given below, a line l intersects two concentric circles at the points A, B, C and D. Prove that AB = CD.
Answer
Draw OM perpendicular to BC.
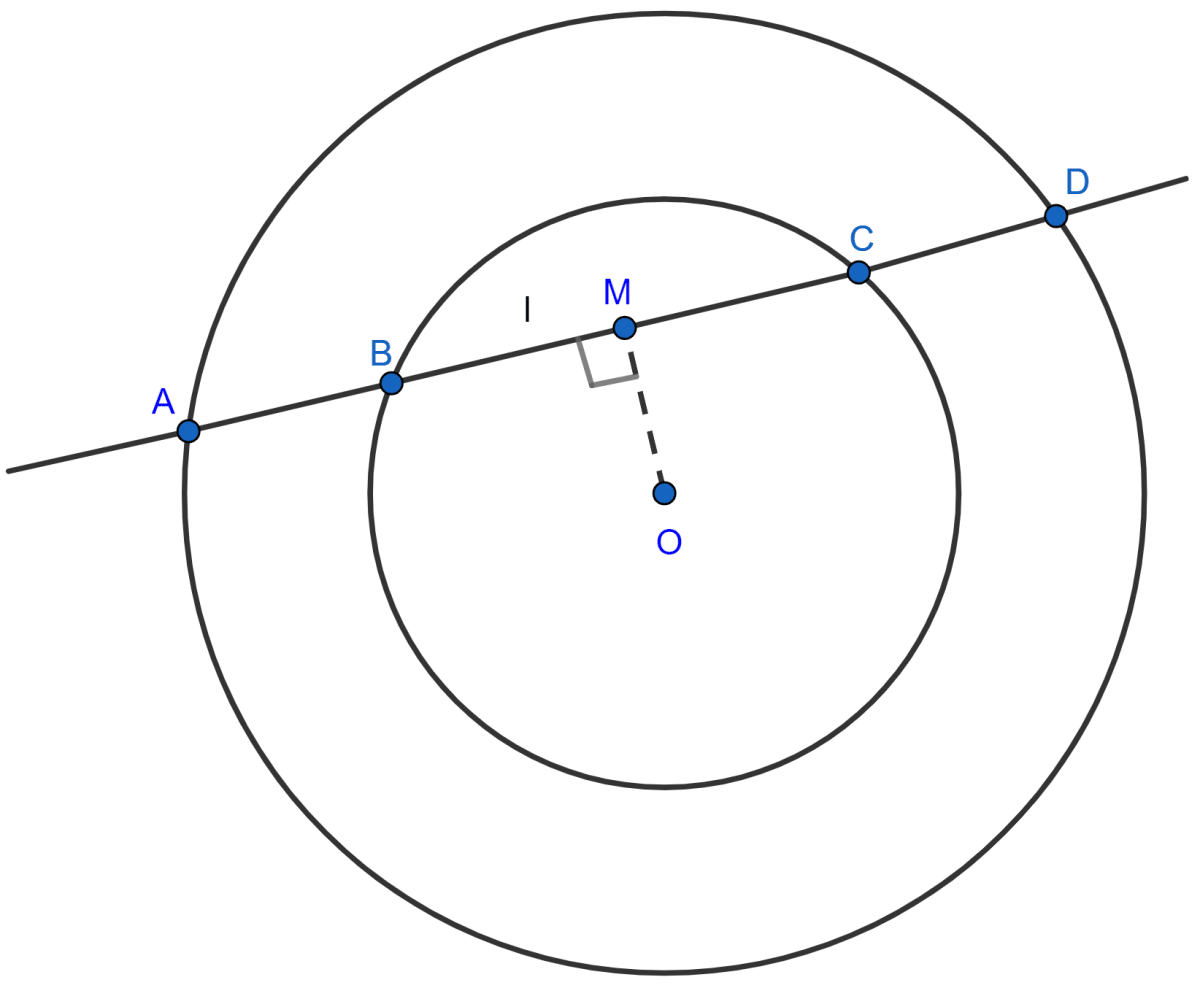
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
So, in the smaller circle, M is mid-point of BC so,
BM = MC = x (let)
Similarly, in larger circle M is mid-point of AD so,
AM = MD = y (let)
From figure,
AB = AM - BM = (y - x)
CD = MD - MC = (y - x)
∴ AB = CD.
Hence, proved that AB = CD.
Related Questions
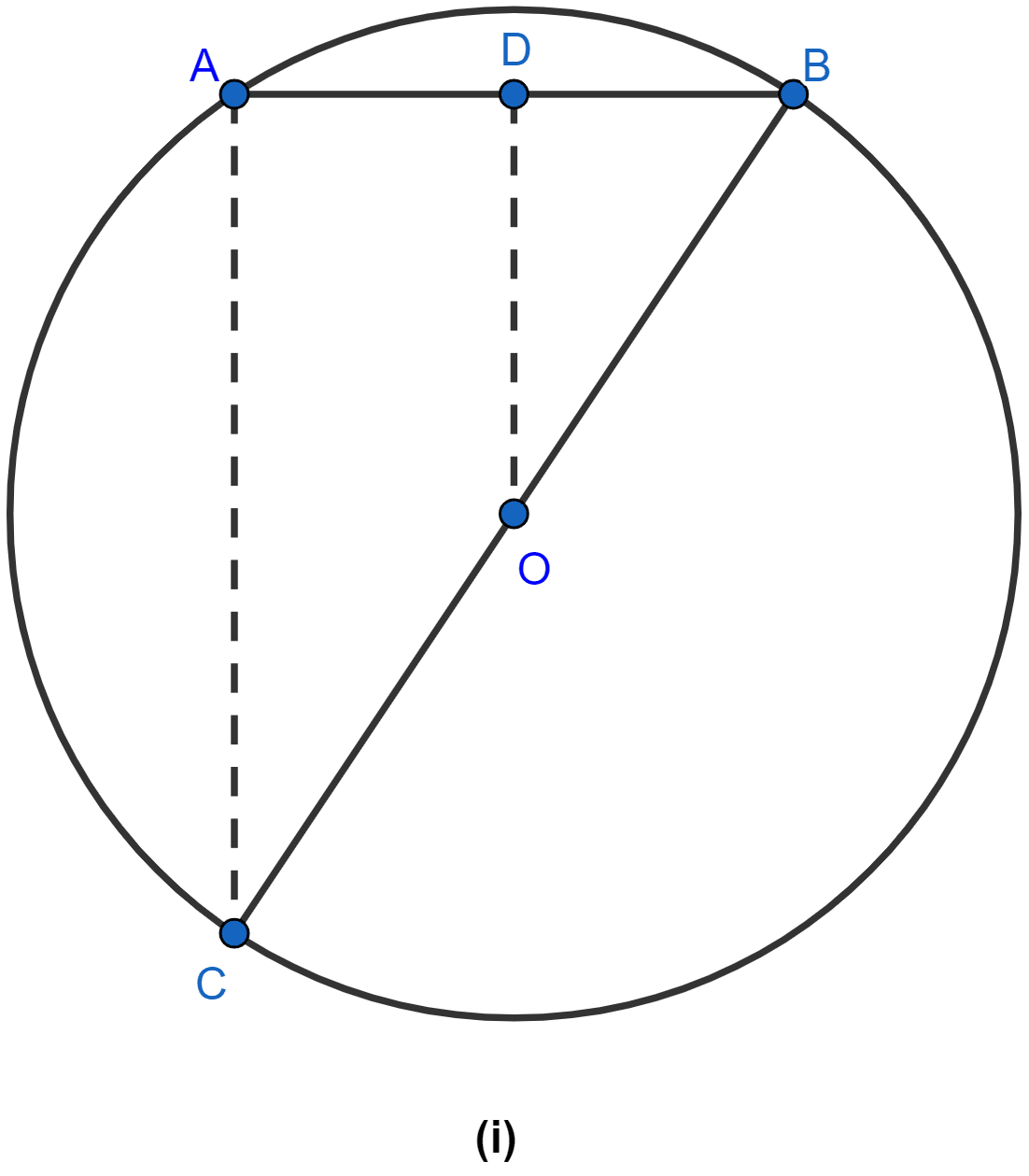
In the figure (i) given below, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2OD.
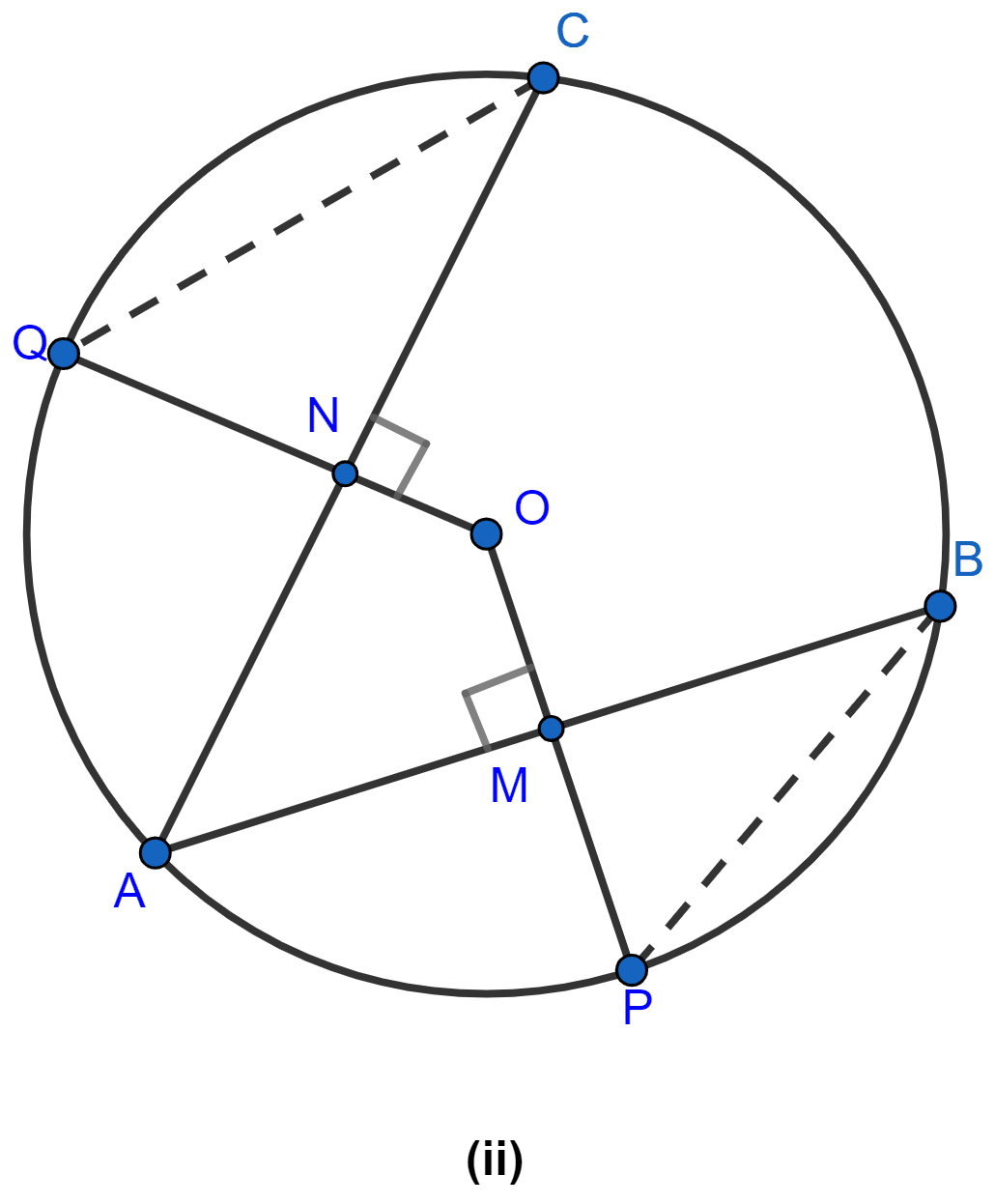
In the figure (ii) given below, chords AB and CD of a circle with centre O intersect at E. If OE bisects ∠AED, prove that AB = CD.

In the figure (i) given below, AD is a diameter of a circle with center O. If AB || CD, prove that AB = CD.

In the figure (ii) given below, O is the center of a circle. If AB and AC are chords of the circle such that AB = AC and OP ⊥ AB, OQ ⊥ AC, prove that PB = QC.