Mathematics
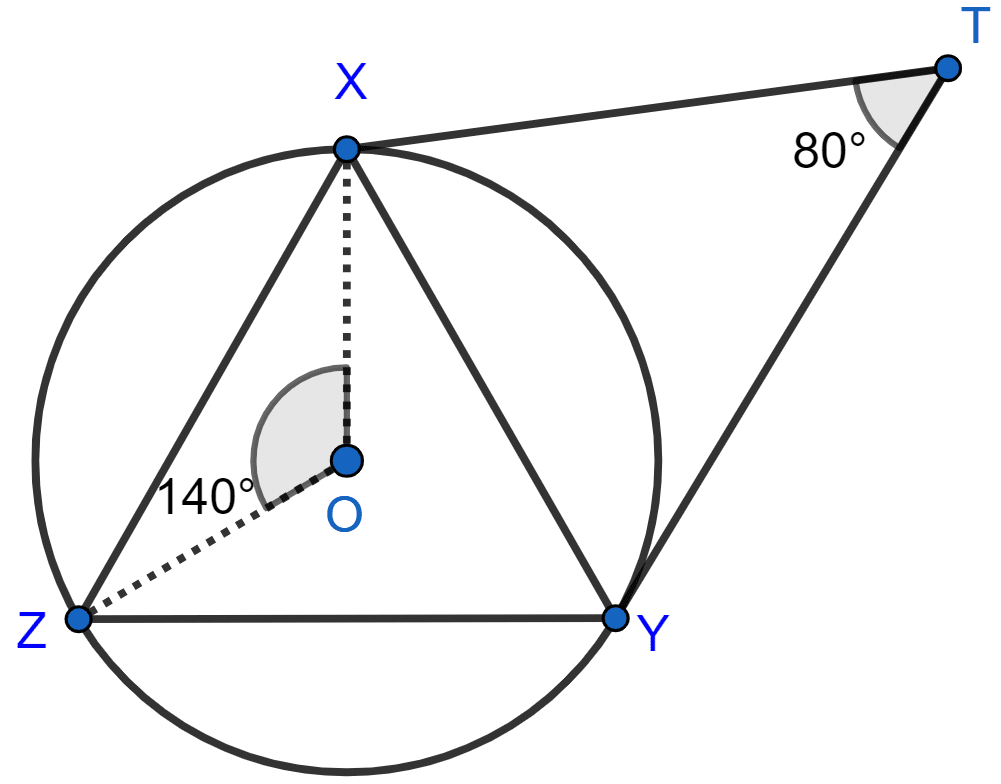
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
Circles
2 Likes
Answer
YT and XT are tangents to the circle.
∴ ∠OYT = 90° and ∠OXT = 90°.
In quadrilateral OYTX,
⇒ ∠XOY + ∠OYT + ∠OXT + ∠XTY = 360°
⇒ ∠XOY + 90° + 90° + 80° = 360°
⇒ ∠XOY = 360° - 260° = 100°.
From figure,
⇒ ∠XOZ + ∠YOZ + ∠XOY = 360°
⇒ 140° + ∠YOZ + 100° = 360°
⇒ ∠YOZ = 360° - 240° = 120°.
We know that,
When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference.
∴ ∠YOZ = 2∠ZXY
⇒ ∠ZXY = ∠YOZ = = 60°.
Hence, ∠ZXY = 60°.
Answered By
2 Likes
Related Questions
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with center O.
Calculate the values of :
(i) ∠QOP
(ii) ∠QCP

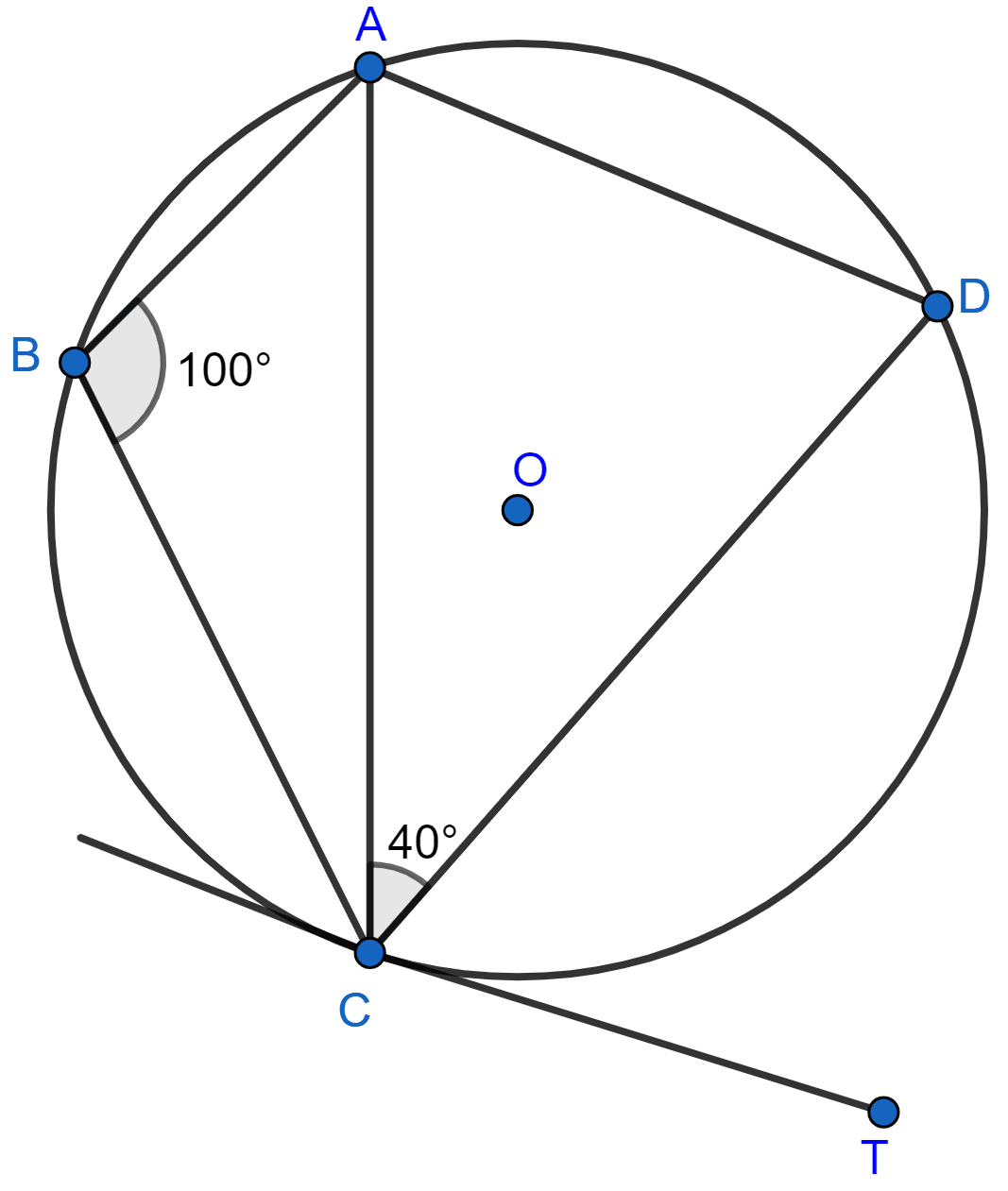
In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.

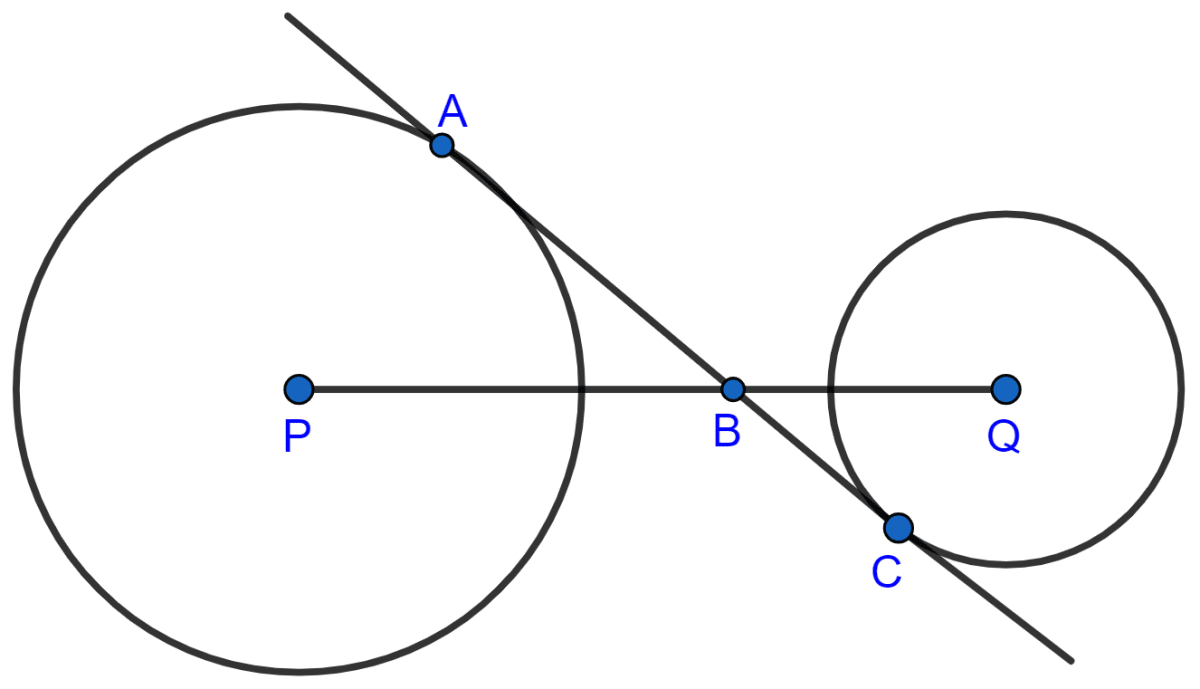
In the figure, given below, AC is a transverse common tangent to two circles with centers P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.