Mathematics
In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate: (i) EF (ii) AC

Similarity
6 Likes
Answer
(i) In ∆PCD and ∆PEF,
∠CPD = ∠EPF [Vertically opposite angles are equal]
∠DCP = ∠FEP [Alternate angles are equal]
∴ ∆PCD ~ ∆PEF [By AA]
Since corresponding sides of similar triangle are proportional to each other.
Hence, EF = 13.5 cm.
(ii) In ∆CEF and ∆CAB
∠FCE = ∠BCA [Common angles]
∠CFE = ∠CBA [As FE || BA, corresponding angles are equal]
∴ ∆CEF ~ ∆CAB [By AA]
Since corresponding sides of similar triangle are proportional to each other.
Hence, AC = 37.5 cm.
Answered By
4 Likes
Related Questions
In the following figure, DE || AC and DC || AP. Prove that : .

In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
(i) Prove that ΔACD is similar to ΔBCA.
(ii) Find BC and CD.
(iii) Find the area of ΔACD : area of ΔABC.
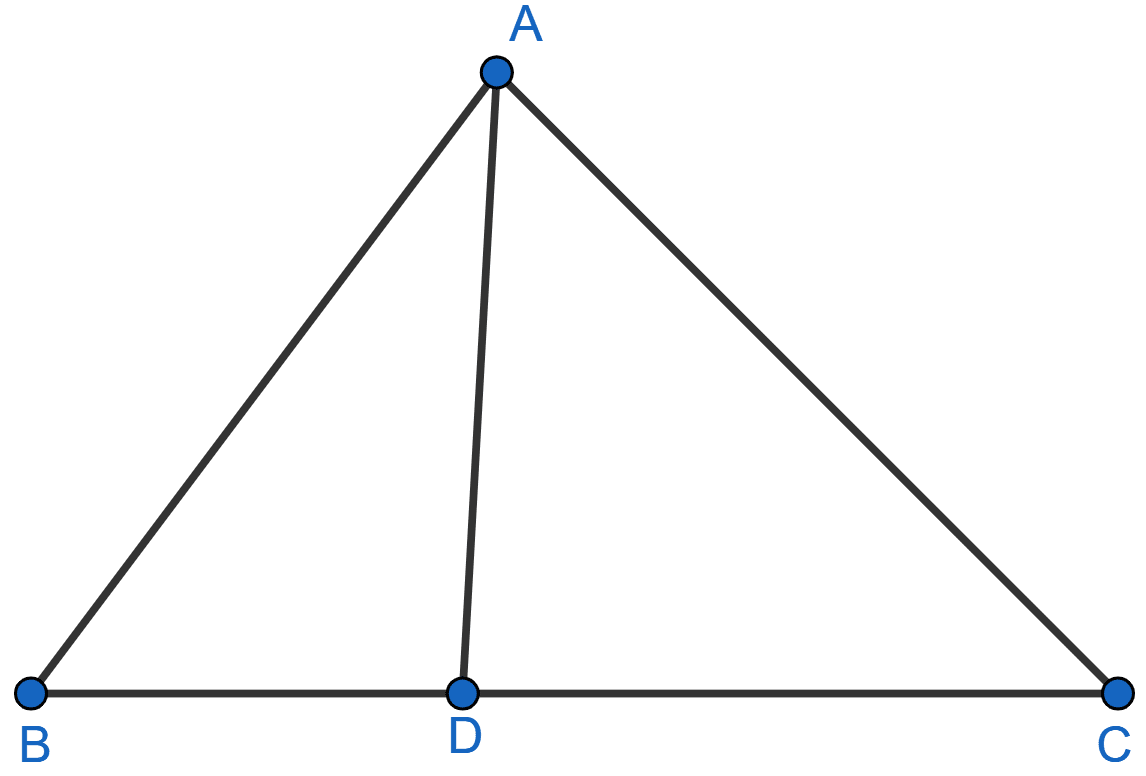
In the following figure, AD and CE are medians of ∆ABC. DF is drawn parallel to CE. Prove that:
(i) EF = FB,
(ii) AG : GD = 2 : 1
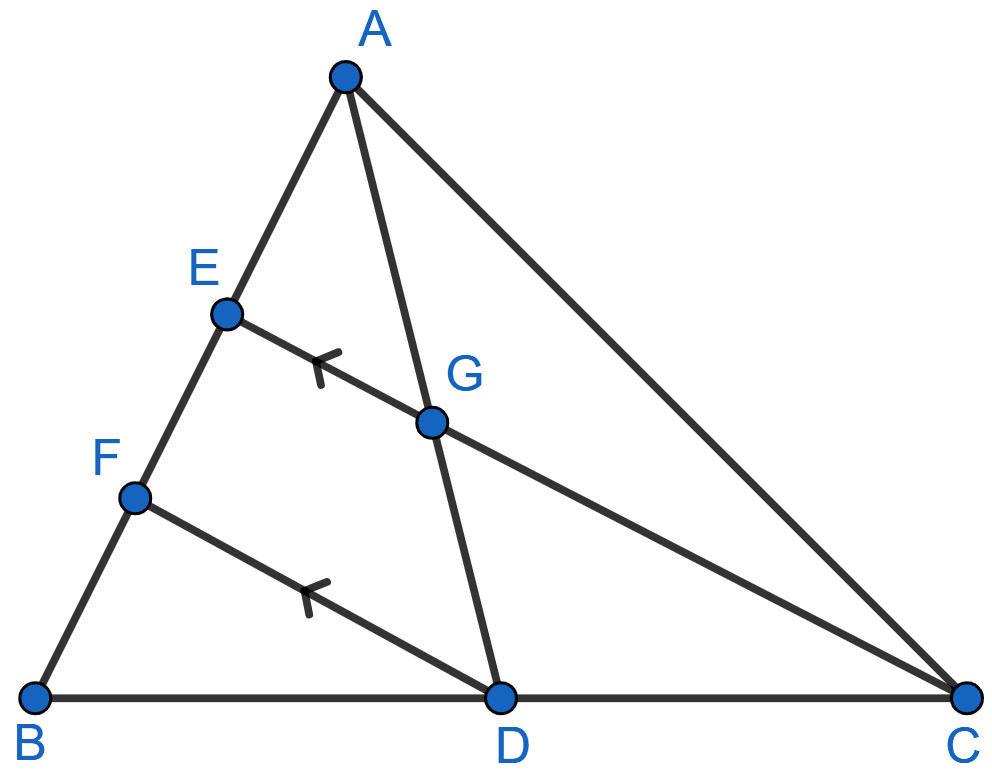
In the following figure, ∠AXY = ∠AYX.
If , show that triangle ABC is isosceles.