Mathematics
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate :
(i) ∠BDC
(ii) ∠BEC
(iii) ∠BAC
Circles
13 Likes
Answer
(i) Given that BD is a diameter of the circle.
We know that,
Angle in a semicircle is a right angle.
So, ∠BCD = 90°
Also given that,
∠DBC = 58°
In ∆BDC,
⇒ ∠DBC + ∠BCD + ∠BDC = 180° [Angle sum property of triangle]
⇒ 58° + 90° + ∠BDC = 180°
⇒ 148° + ∠BDC = 180°
⇒ ∠BDC = 180° - 148° = 32°.
Hence, ∠BDC = 32°.
(ii) We know that, the opposite angles of a cyclic quadrilateral are supplementary.
So, in cyclic quadrilateral BECD
⇒ ∠BEC + ∠BDC = 180°
⇒ ∠BEC + 32° = 180°
⇒ ∠BEC = 180° - 32° = 148°
Hence, ∠BEC = 148°.
(iii) In cyclic quadrilateral ABEC,
⇒ ∠BAC + ∠BEC = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]
⇒ ∠BAC + 148° = 180°
⇒ ∠BAC = 180° - 148°= 32°.
Hence, ∠BAC = 32°.
Answered By
8 Likes
Related Questions
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
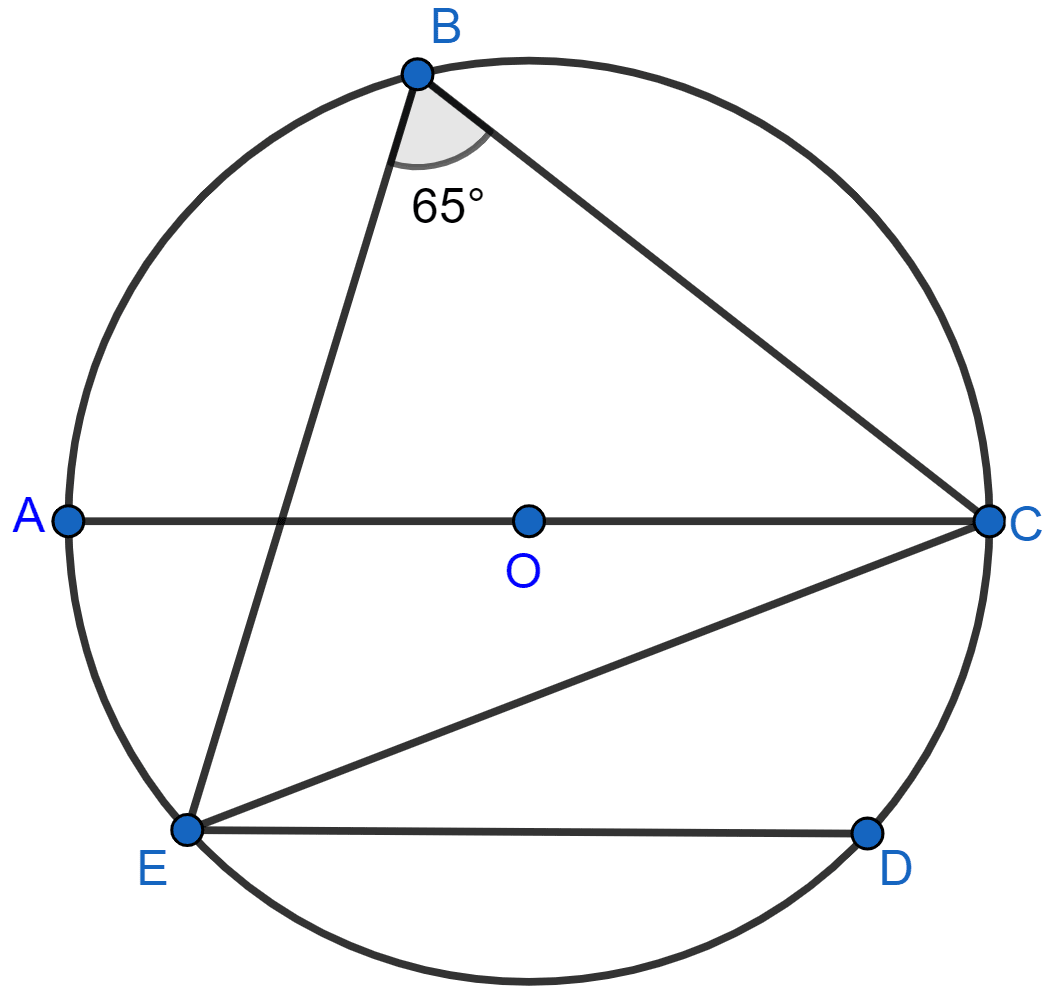
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Given reason in support of your answer.
