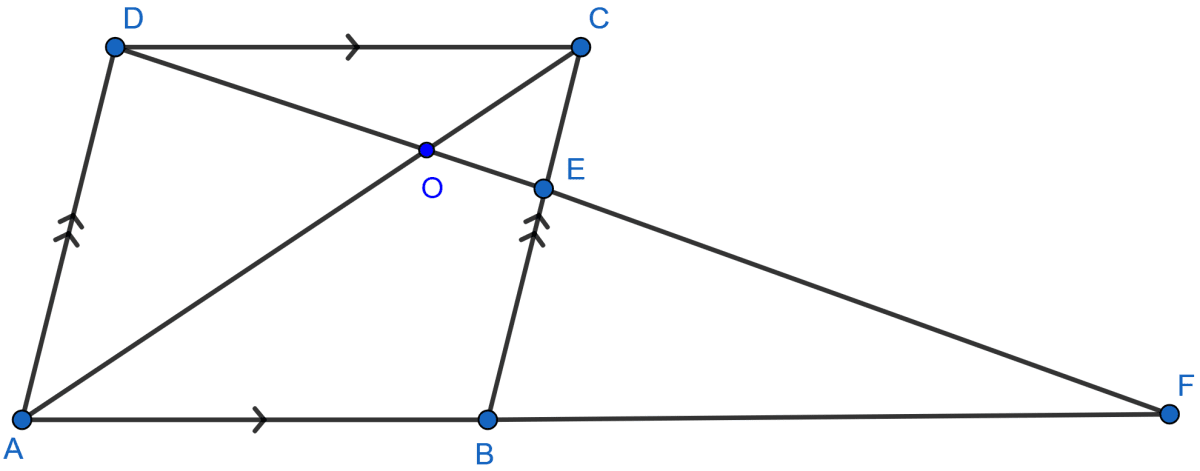
In the adjoining figure, the diagonals of a parallelogram intersect at O. OE is drawn parallel to CB to meet AB at E, find area of △AOE : area of ||gm ABCD.

In the figure,

Diagonals of parallelogram ABCD are AC and BD which intersect each other at O. OE is drawn parallel to CB to meet AB in E.

In the figure four triangles have equal area.

So, Area of △OAB = $\dfrac{1}{4}$ Area of parallelogram ABCD

Then, O is the midpoint of AC as diagonals of parallelogram intersect at centre.
OE || CB. We know that, ABCD is a parallelogram and opposite sides are parallel in parallelogram. Thus OE || AD also,

∴ E is the midpoint of AB.

∴ OE is the median of △AOB.

$\text{Area of △AOE} = \dfrac{1}{2} \text{Area of △AOB} \\[1em] = \dfrac{1}{2} \times \dfrac{1}{4} \text{Area of parallelogram ABCD} \\[1em] = \dfrac{1}{8} \text{Area of parallelogram ABCD} \\[1em] \therefore \text{Area of △AOE} = \dfrac{1}{8} \text{Area of parallelogram ABCD} \\[1em] \therefore \dfrac{\text{Area of △AOE}}{\text{Area of parallelogram ABCD}} = \dfrac{1}{8}.$

Hence, the ratio of area of △AOE : area of ||gm ABCD is 1 : 8.