Mathematics
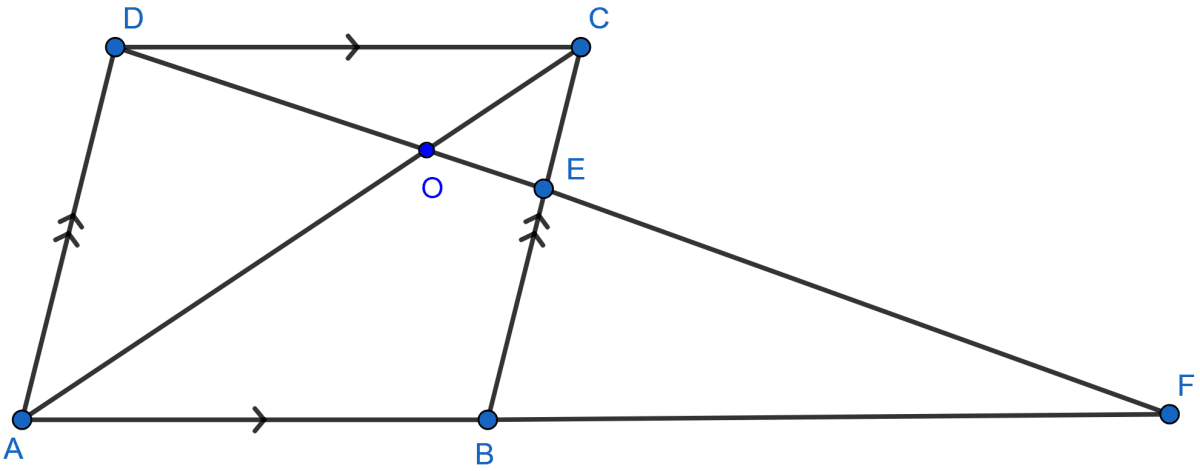
In the adjoining figure, the diagonals of a parallelogram intersect at O. OE is drawn parallel to CB to meet AB at E, find area of △AOE : area of ||gm ABCD.
Similarity
44 Likes
Answer
In the figure,
Diagonals of parallelogram ABCD are AC and BD which intersect each other at O. OE is drawn parallel to CB to meet AB in E.
In the figure four triangles have equal area.
So, Area of △OAB = Area of parallelogram ABCD
Then, O is the midpoint of AC as diagonals of parallelogram intersect at centre.
OE || CB. We know that, ABCD is a parallelogram and opposite sides are parallel in parallelogram. Thus OE || AD also,
∴ E is the midpoint of AB.
∴ OE is the median of △AOB.
Hence, the ratio of area of △AOE : area of ||gm ABCD is 1 : 8.
Answered By
28 Likes
Related Questions
If the areas of two similar triangles are 360 cm2 and 250 cm2 and if one side of the first triangle is 8 cm, find the length of the corresponding side of the second triangle.
In the adjoining figure, D is a point on BC such that ∠ABD = ∠CAD. If AB = 5 cm, AC = 3 cm and AD = 4 cm, find
(i) BC
(ii) DC
(iii) area of △ACD : area of △BCA

In the adjoining figure, ABCD is a trapezium in which AB || DC. If 2AB = 3DC, find the ratio of the areas of △AOB and △COD.

In the adjoining figure, ABCD is a parallelogram. E is mid-point of BC. DE meets the diagonal AC at O and meet AB (produced) at F. Prove that
(i) DO : OE = 2 : 1
(ii) area of △OEC : area of △OAD = 1 : 4