Mathematics
In the adjoining figure, OA ⊥ OD, OC ⊥ OB, OD = OA and OB = OC. Prove that AB = CD.
Answer
From figure,
∠AOD = ∠COB (Each 90°)
Adding ∠AOC to both sides,
⇒ ∠AOD + ∠AOC = ∠AOC + ∠COB
⇒ ∠COD = ∠AOB.
Now, in △AOB and △DOC
OA = OD (Given)
OB = OC (Given)
∠AOB = ∠COD (Proved)
∴ △AOB ≅ △DOC (SAS axiom)
We know that corresponding parts of congruent triangles are equal.
∴ AB = CD.
Hence, proved that AB = CD.
Related Questions
In triangles ABC and DEF, ∠A = ∠D, ∠B = ∠E and AB = EF. Will the two triangles be congruent? Give reasons for your answer.
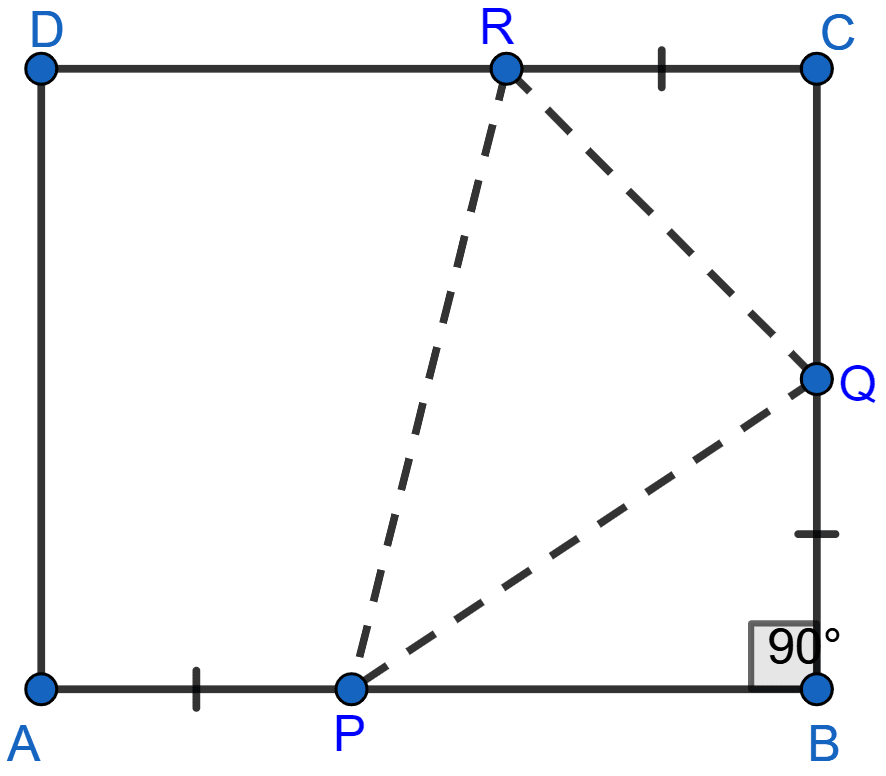
In the adjoining figure, AB = AC, D is a point in the interior of △ABC such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of △ABC.
In the adjoining figure, PQ || BA and RS || CA. If BP = RC, prove that:
(i) △BSR ≅ △PQC
(ii) BS = PQ
(iii) RS = CQ.
In the adjoining figure, ABCD is a square. P, Q and R are points on the sides AB, BC and CD respectively such that AP = BQ = CR and ∠PQR = 90°. Prove that
(a) △PBQ ≅ △QCR
(b) PQ = QR
(c) ∠PRQ = 45°
