Mathematics
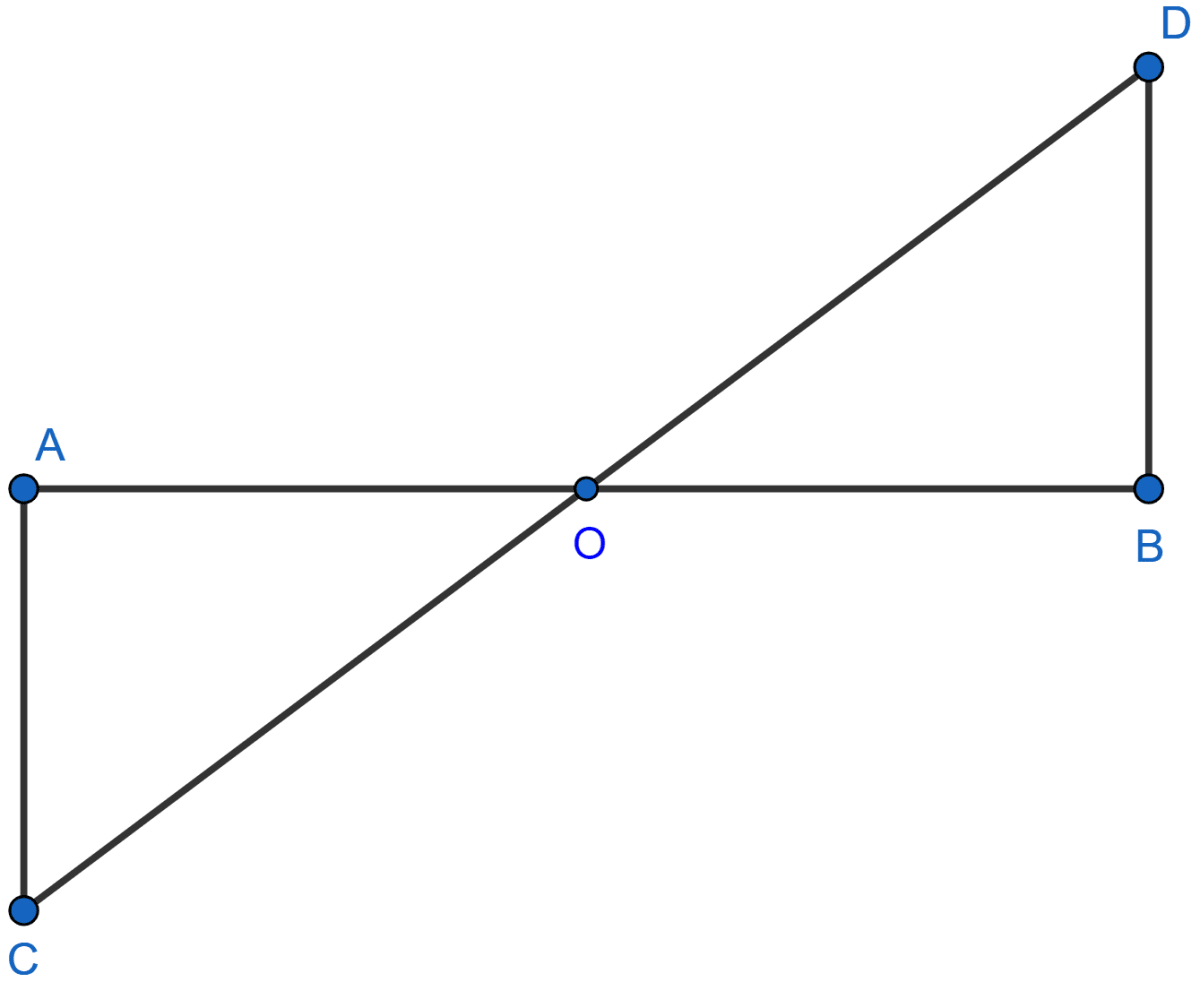
In the adjoining figure, O is the mid-point of AB. If ∠ACO = ∠BDO, then ∠OAC is equal to
∠OCA
∠ODB
∠OBD
∠BOD
Triangles
13 Likes
Answer
In △AOC and △BOD,
AO = OB (As O is the mid-point of AB.)
∠ACO = ∠BDO (Given)
∠AOC = ∠BOD (Vertically opposite angles)
Hence, △AOC ≅ △BOD by AAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ ∠OAC = ∠OBD.
Hence, Option 3 is the correct answer.
Answered By
7 Likes
Related Questions
In the adjoining figure, ABCD is a quadrilateral in which BN and DM are drawn perpendiculars to AC such that BN = DM. If OB = 4 cm, then BD is
6 cm
8 cm
10 cm
12 cm
In the adjoining figure, AB ⊥ BE and FE ⊥ BE. If AB = FE and BC = DE, then
△ABD ≅ △EFC
△ABD ≅ △FEC
△ABD ≅ △ECF
△ABD ≅ △CEF
In the adjoining figure, AC = BD. If ∠CAB = ∠DBA, then ∠ACB is equal to
∠BAD
∠ABC
∠ABD
∠BDA
In the adjoining figure, AB = AC and AD is median of △ABC, then ∠ADC is equal to
60°
120°
90°
75°
