Mathematics
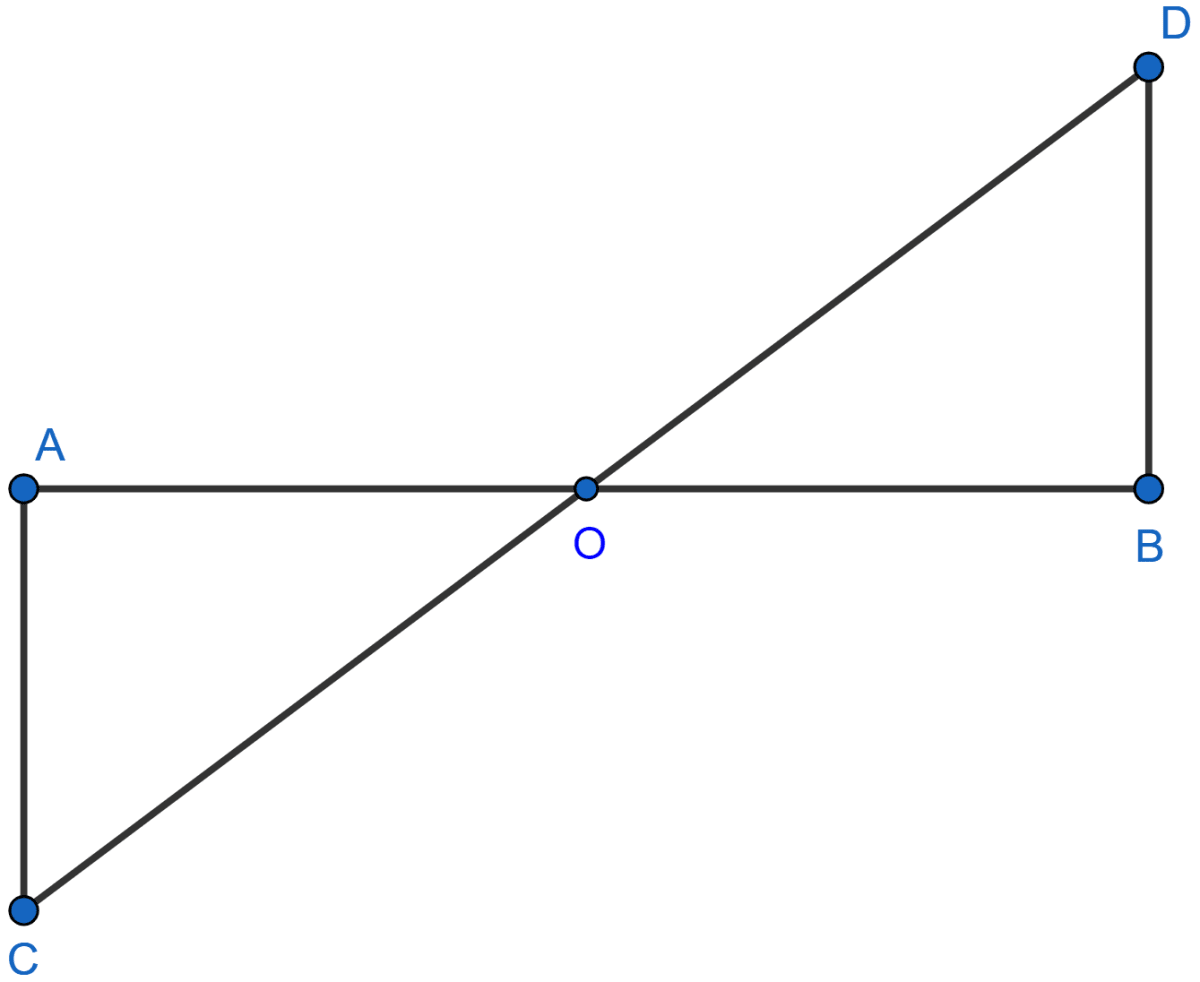
In the adjoining figure, AB ⊥ BE and FE ⊥ BE. If AB = FE and BC = DE, then
△ABD ≅ △EFC
△ABD ≅ △FEC
△ABD ≅ △ECF
△ABD ≅ △CEF
Triangles
ICSE
7 Likes
Answer
In △ABD and △FEC,
Given,
⇒ BC = ED
⇒ BC + CD = ED + CD
⇒ BD = EC.
AB = FE (Given)
∠ABD = ∠FEC (Both are equal to 90°)
Hence, △ABD ≅ △FEC by SAS axiom.
Hence, Option 2 is the correct answer.
Answered By
4 Likes
Related Questions
In the adjoining figure, AB = AC and AD is median of △ABC, then ∠ADC is equal to
60°
120°
90°
75°
Which of the following is not a criterion for congruency of triangles?
SAS
ASA
SSA
SSS
In the adjoining figure, AB = FC, EF = BD and ∠AFE = ∠CBD. Then the rule by which △AFE ≅ △CBD is
SAS
ASA
SSS
AAS
In the adjoining figure, O is the mid-point of AB. If ∠ACO = ∠BDO, then ∠OAC is equal to
∠OCA
∠ODB
∠OBD
∠BOD
