Mathematics
In the adjoining figure, D and E are points on the side BC of △ABC such that BD = EC and AD = AE. Show that △ABD ≅ △ACE.

Triangles
28 Likes
Answer
Given, AD = AE.
∴ ∠ADE = ∠AED (As angles opposite to equal sides are equal.)
⇒ 180 - ∠ADE = 180 - ∠AED
⇒ ∠ADB = ∠AEC.
BD = EC (Given)
∴ △ABD ≅ △ACE by SAS axiom.
Hence, proved that △ABD ≅ △ACE.
Answered By
18 Likes
Related Questions
In a triangle ABC, AB = AC, D and E are points on the sides AB and AC respectively such that BD = CE. Show that:
(i) △DBC ≅ △ECB
(ii) ∠DCB = ∠EBC
(iii) OB = OC, where O is the point of intersection of BE and CD.
ABC is an isosceles triangle in which AB = AC. P is any point in the interior of △ABC such that ∠ABP = ∠ACP. Prove that
(a) BP = CP
(b) AP bisects ∠BAC.
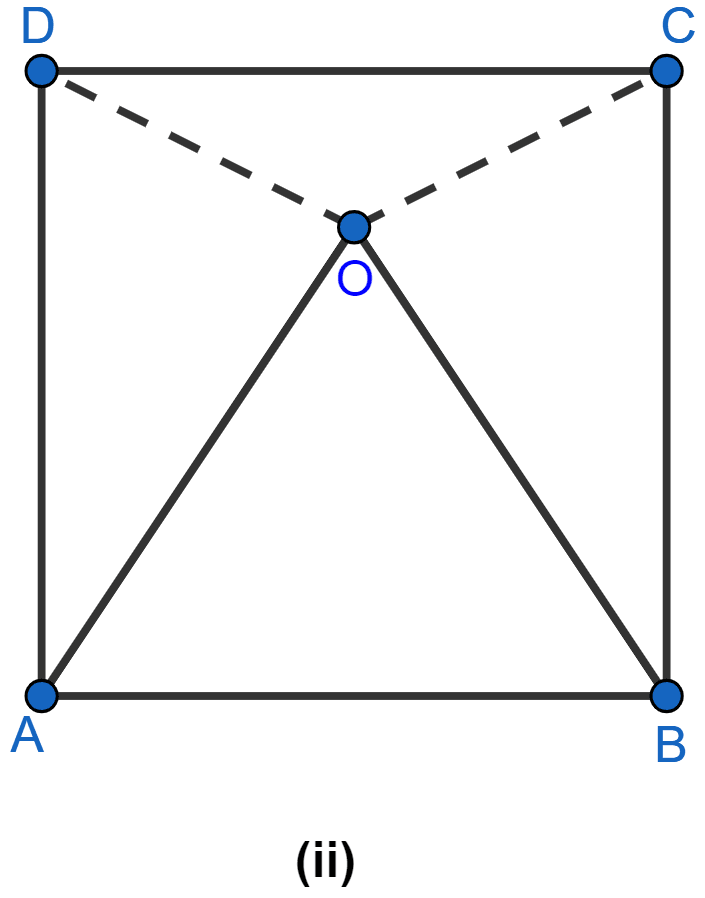
In the figure (i) given below, CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that △ADE ≅ △BCE and hence, AEB is an isosceles triangle.
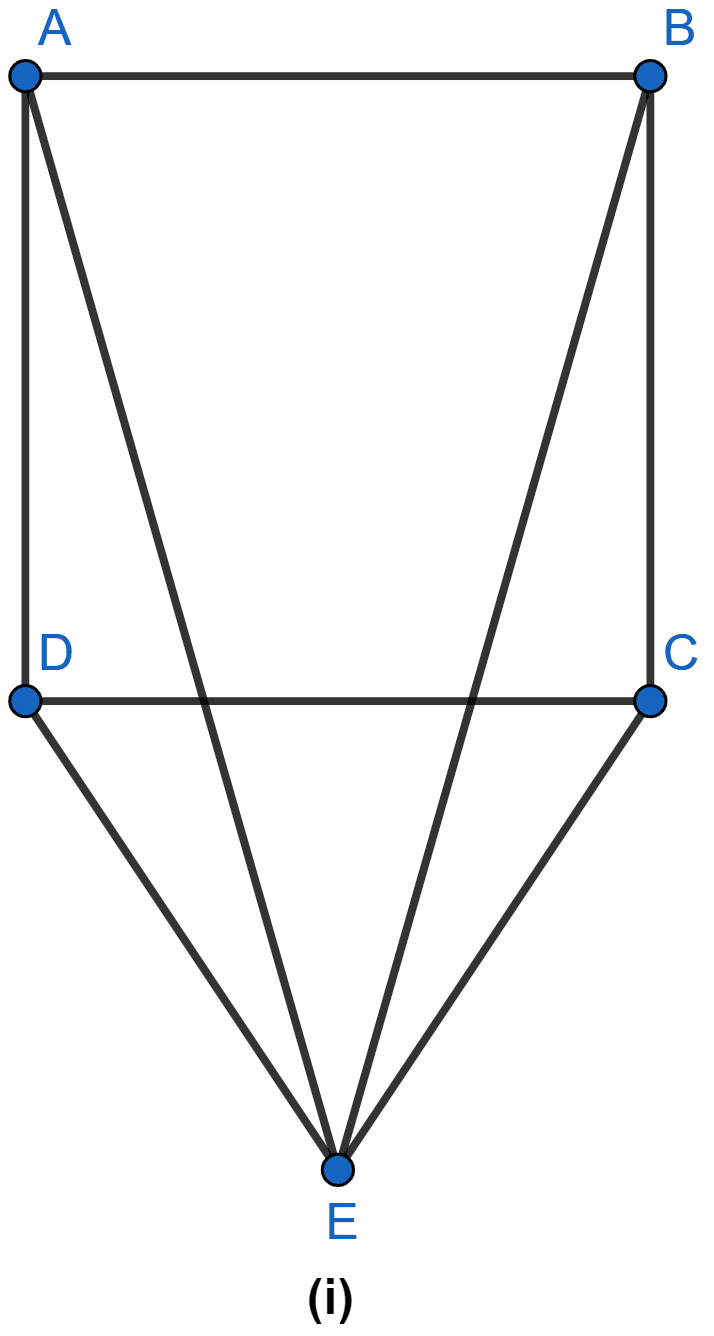
In the figure (ii) given below, O is the point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that OCD is an isosceles triangle.