Mathematics
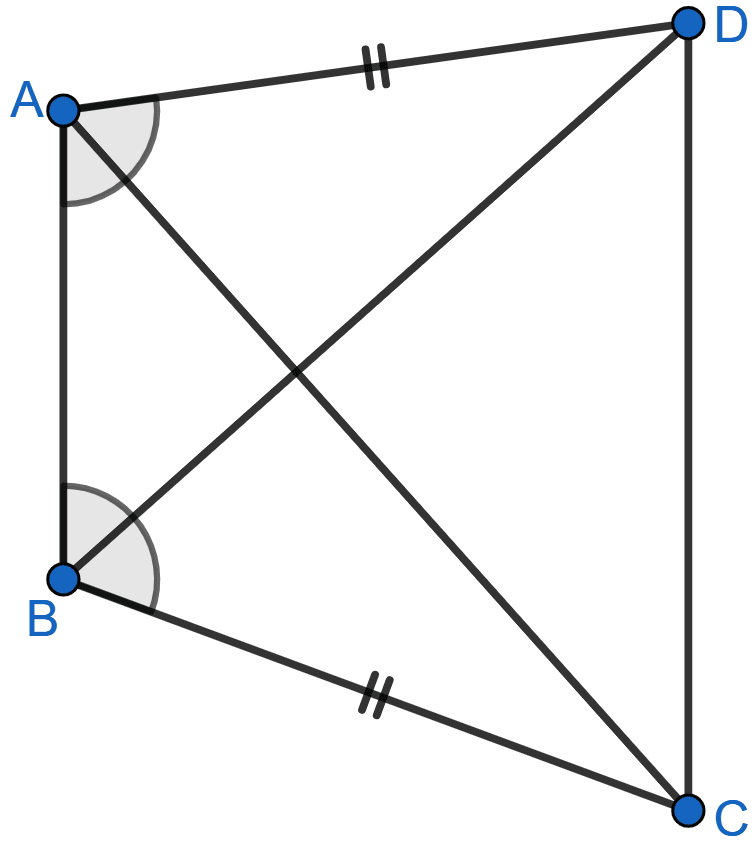
In the adjoining figure, ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA. Prove that
(i) △ABD ≅ △BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC
Triangles
38 Likes
Answer
(i) In △ABD and △BAC,
AD = BC (Given)
∠BAD = ∠ABC (Given)
AB = AB (Common sides)
Hence, by SAS axiom △ABD ≅ △BAC.
(ii) As, △ABD ≅ △BAC.
We know that corresponding sides of congruent triangles are equal.
∴ BD = AC.
Hence, proved that BD = AC.
(iii) As, △ABD ≅ △BAC.
We know that corresponding angles of congruent triangles are equal.
∴ ∠ABD = ∠BAC.
Hence, proved that ∠ABD = ∠BAC.
Answered By
23 Likes
Related Questions
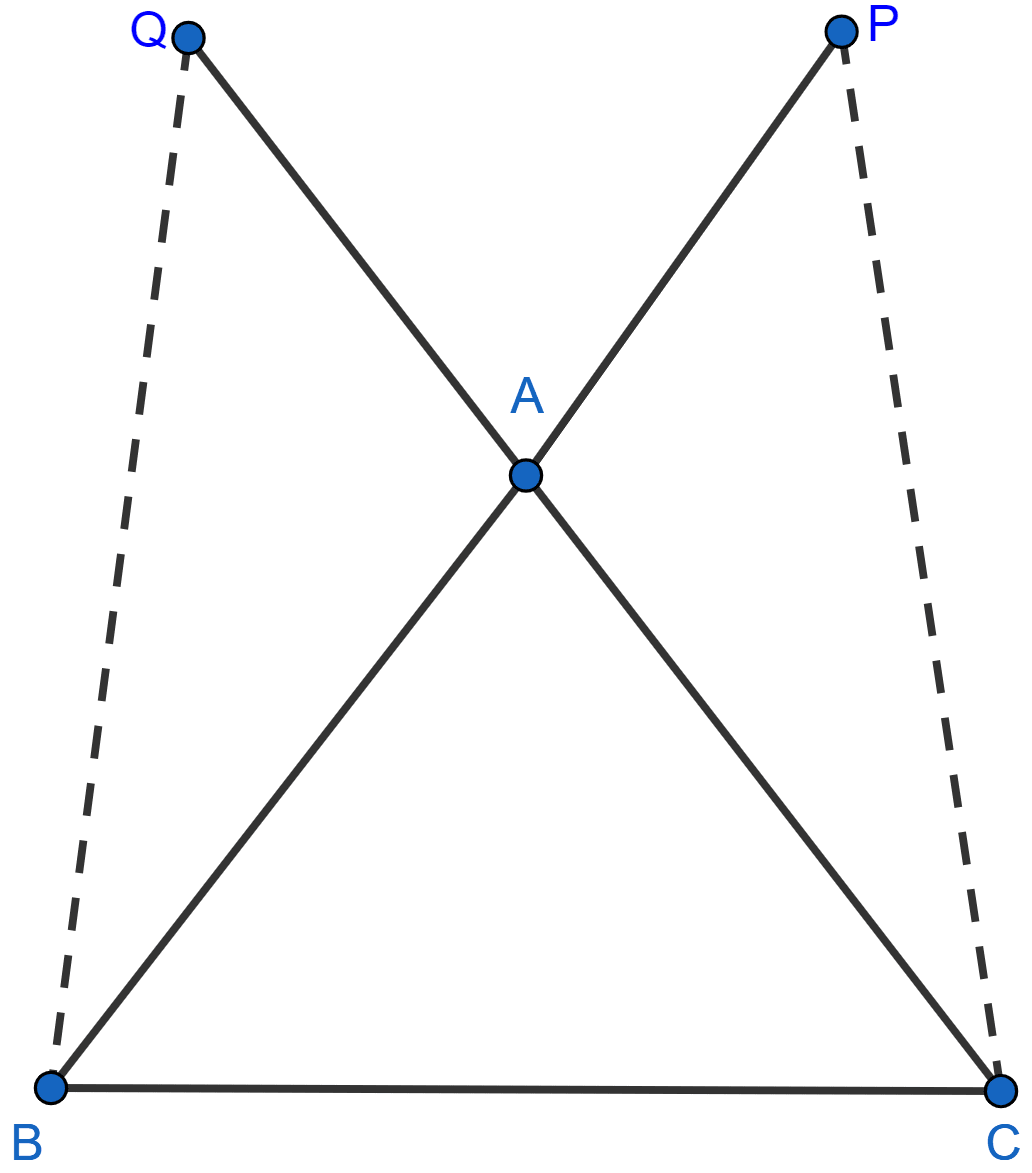
In the adjoining figure, AB = AC, P and Q are points on BA and CA respectively such that AP = AQ. Prove that
(i) △APC ≅ △AQB
(ii) CP = BQ
(iii) ∠ACP = ∠ABQ.
In the adjoining figure, AD = BC and BD = AC. Prove that:
∠ADB = ∠BCA and ∠DAB = ∠CBA.

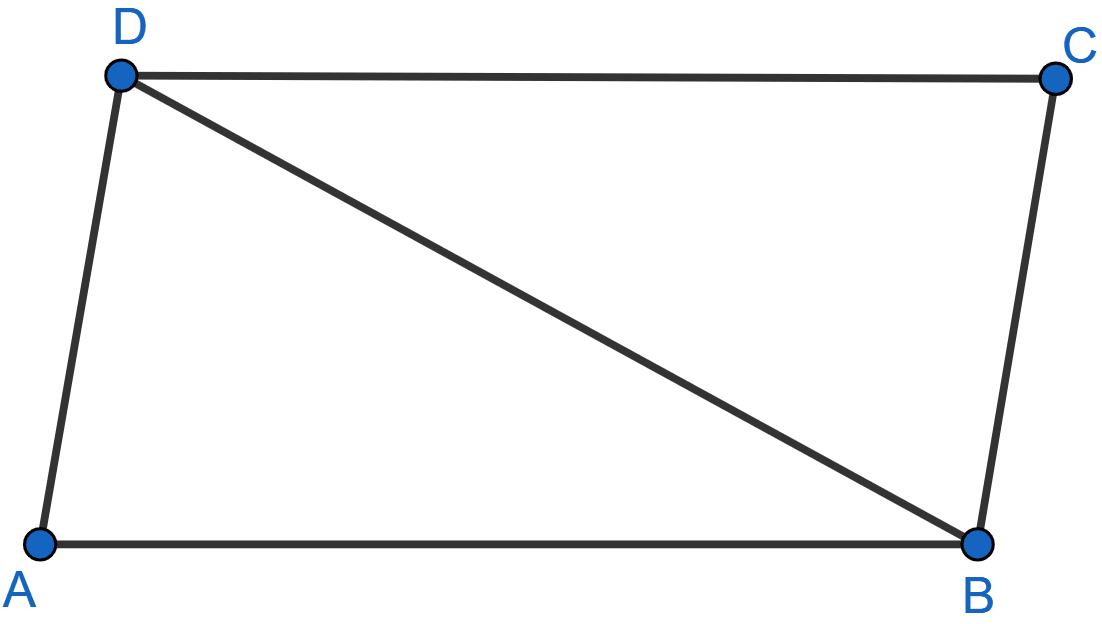
In the adjoining figure, AB = DC and AB || DC. Prove that AD = BC.
In the adjoining figure AC = AE, AB = AD and ∠BAD = ∠CAE. Show that BC = DE.
