Mathematics
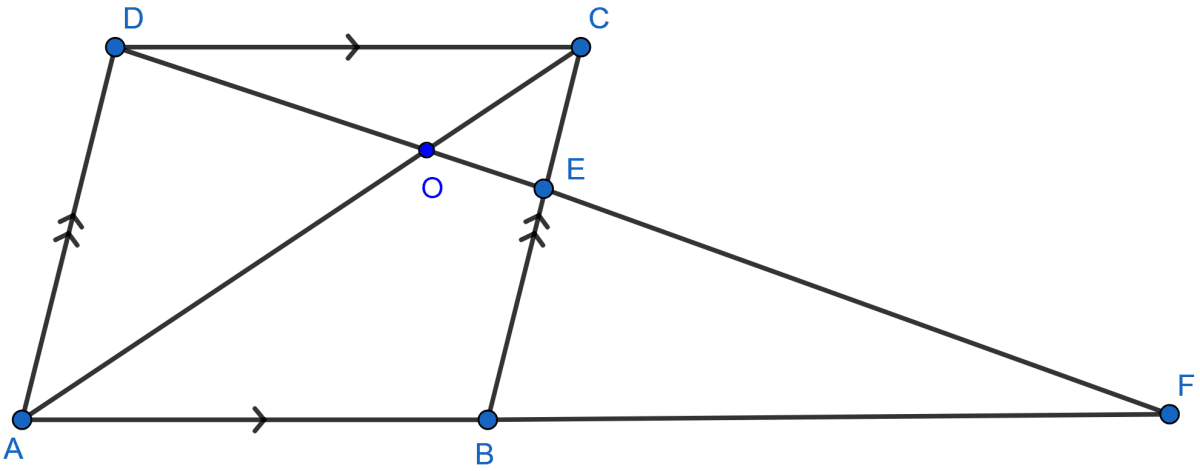
In the adjoining figure, ABCD is a parallelogram. E is mid-point of BC. DE meets the diagonal AC at O and meet AB (produced) at F. Prove that
(i) DO : OE = 2 : 1
(ii) area of △OEC : area of △OAD = 1 : 4
Similarity
24 Likes
Answer
(i) Given E is the mid-point of BC,
∴ 2EC = BC
Since ABCD is a parallelogram so, BC = AD or, 2EC = AD.
Considering △AOD and △EDC,
∠AOD = ∠EOC (Vertically opposite angles are equal)
∠OAD = ∠OCB (Alternate angles are equal)
Hence by AA axiom △AOD ~ △EOC. Since triangles are similar so the ratio of their corresponding sides are equal.
Hence, proved that DO : OE = 2 : 1.
(ii) From (i) we have proved that △AOD ~ △EOC.
Hence, proved that area of △OEC : area of △OAD = 1 : 4.
Answered By
15 Likes
Related Questions
In the adjoining figure, D is a point on BC such that ∠ABD = ∠CAD. If AB = 5 cm, AC = 3 cm and AD = 4 cm, find
(i) BC
(ii) DC
(iii) area of △ACD : area of △BCA

In the adjoining figure, the diagonals of a parallelogram intersect at O. OE is drawn parallel to CB to meet AB at E, find area of △AOE : area of ||gm ABCD.
In the adjoining figure, ABCD is a trapezium in which AB || DC. If 2AB = 3DC, find the ratio of the areas of △AOB and △COD.

A model of a ship is made to a scale of 1 : 250. Calculate :
(i) the length of the ship, if the length of model is 1.6 m.
(ii) the area of the deck of the ship, if the area of the deck of model is 2.4 m2.
(iii) the volume of the model, if the volume of the ship is 1 km3.