Mathematics
In the adjoining figure, ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.

Answer
In △ABC, ∠A = 90° and AB = AC.
⇒ ∠B = ∠C (As angles opposite to equal sides are equal)
We know,
∠A + ∠B + ∠C = 180°
90° + ∠B + ∠B = 180°
2∠B = 90°
∠B = 45° .
As AD is bisector of ∠A, ∠BAD = ∠CAD = 45°.
AD = AD (Common)
∠ACD = ∠ABD = 45°
Hence, △ABD ≅ △ACD by AAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ BD = CD ………(i)
In △ABD, ∠BAD = ∠ABD (each = 45°)
⇒ AD = BD (As sides opposite to equal angles are equal) ……..(ii)
∴ BC = BD + CD
= BD + BD (Using (i))
∴ BC = 2BD
Using (ii),
BC = 2AD.
Hence, proved that BC = 2AD.
Related Questions
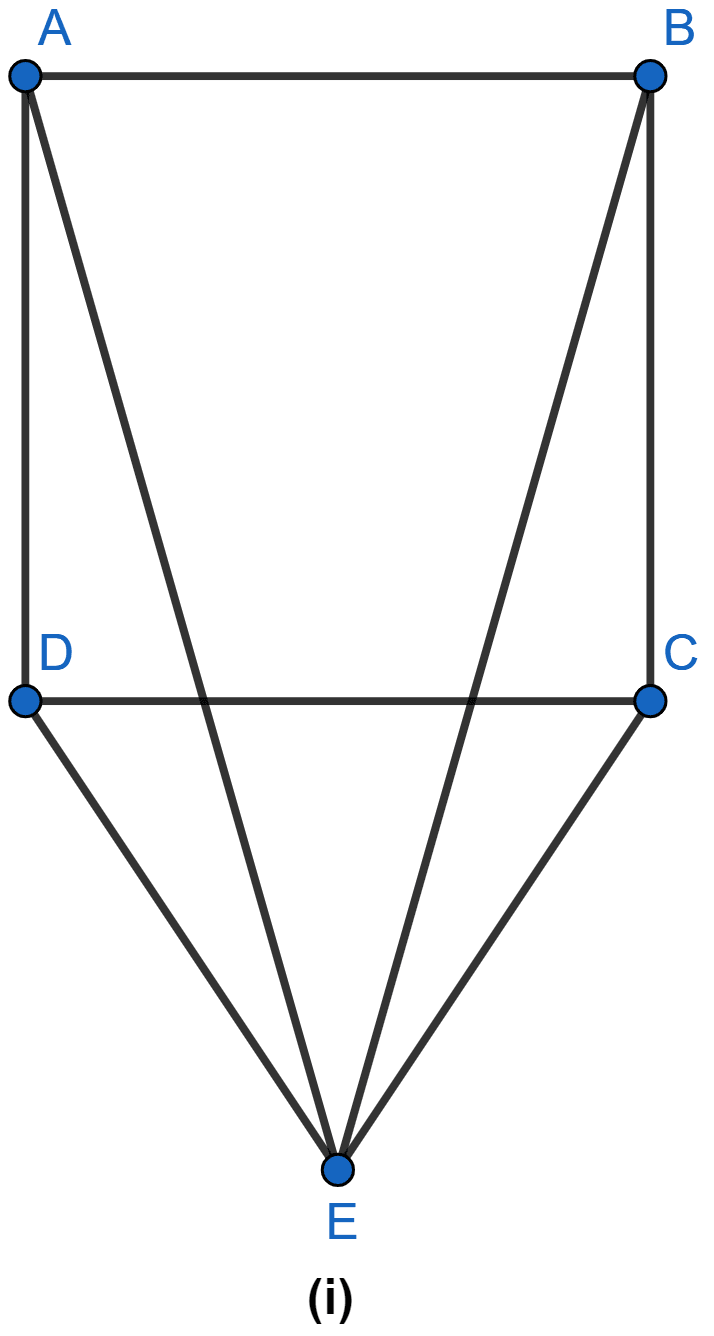
In the figure (i) given below, CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that △ADE ≅ △BCE and hence, AEB is an isosceles triangle.
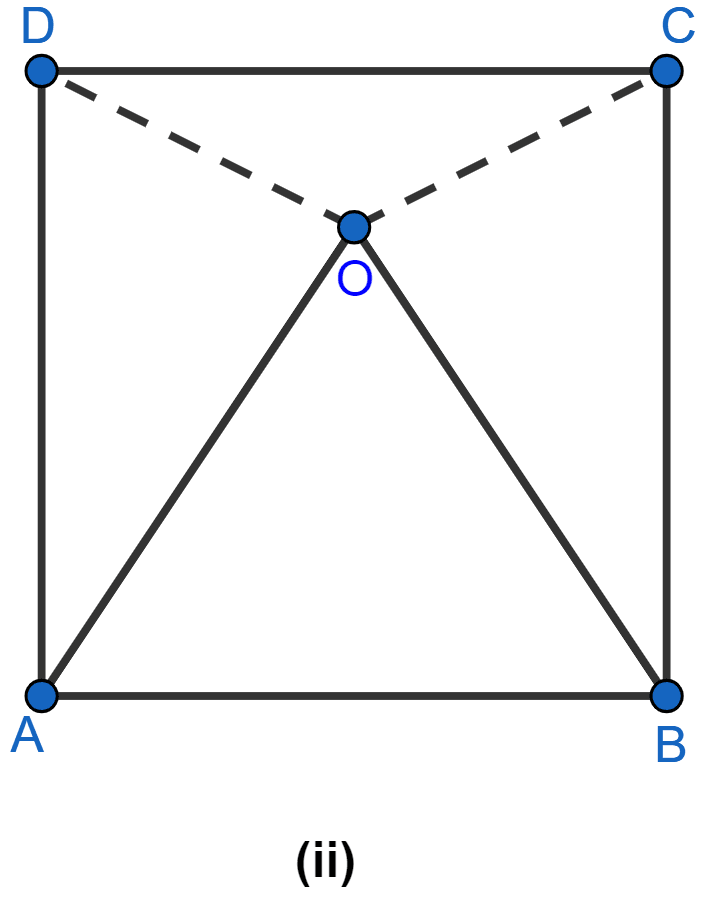
In the figure (ii) given below, O is the point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that OCD is an isosceles triangle.
In △PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is longest? Give reason for your answer.
Show that in a right angled triangle, the hypotenuse is the longest side.