Mathematics
In the adjoining figure, ABC is a right angled triangle at B. A semicircle is drawn on AB as diameter. If AB = 12 cm and BC = 5 cm, then the area of the shaded region is
(60 + 18π) cm2
(30 + 36π) cm2
(30 + 18π) cm2
(30 + 9π) cm2

Mensuration
4 Likes
Answer
Area of right angle triangle ABC = × base × height
= × AB × BC
= × 12 × 5
= 30 cm2.
From figure,
AB = 12 cm is the diameter of circle.
Radius = = 6 cm.
Area of semi-circle = = 18π cm2.
Area of shaded region = Area of right angle triangle ABC + Area of semi-circle
= (30 + 18π) cm2.
Hence, Option 3 is the correct option.
Answered By
2 Likes
Related Questions
In the adjoining figure, the boundary of the shaded region consists of semicircular arcs. The area of the shaded region is equal to
616 cm2
385 cm2
231 cm2
308 cm2
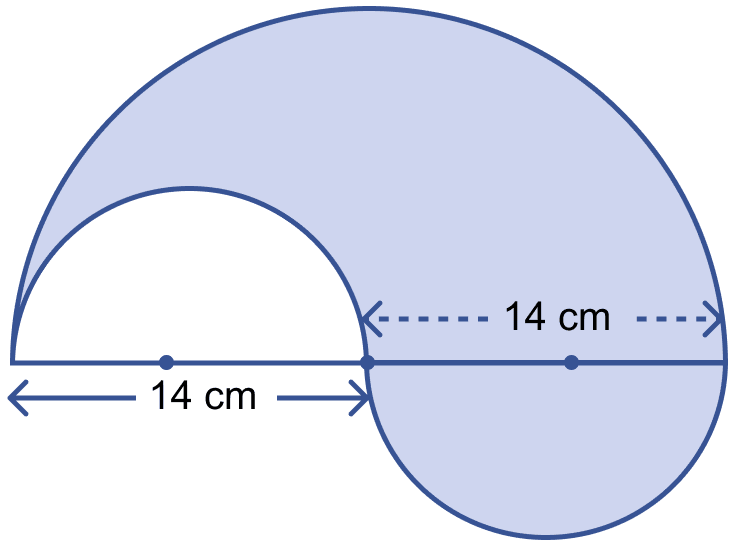
The perimeter of the shaded region shown in the below figure is
44 cm
88 cm
66 cm
132 cm

The perimeter of the shaded region shown in the below figure is
(30 + 6π) cm
(30 + 12π) cm
(18 + 12π) cm
(18 + 6π) cm

If the volume of a cube is 729 m3, then its surface area is
486 cm2
324 cm2
162 cm2
None of these