Mathematics
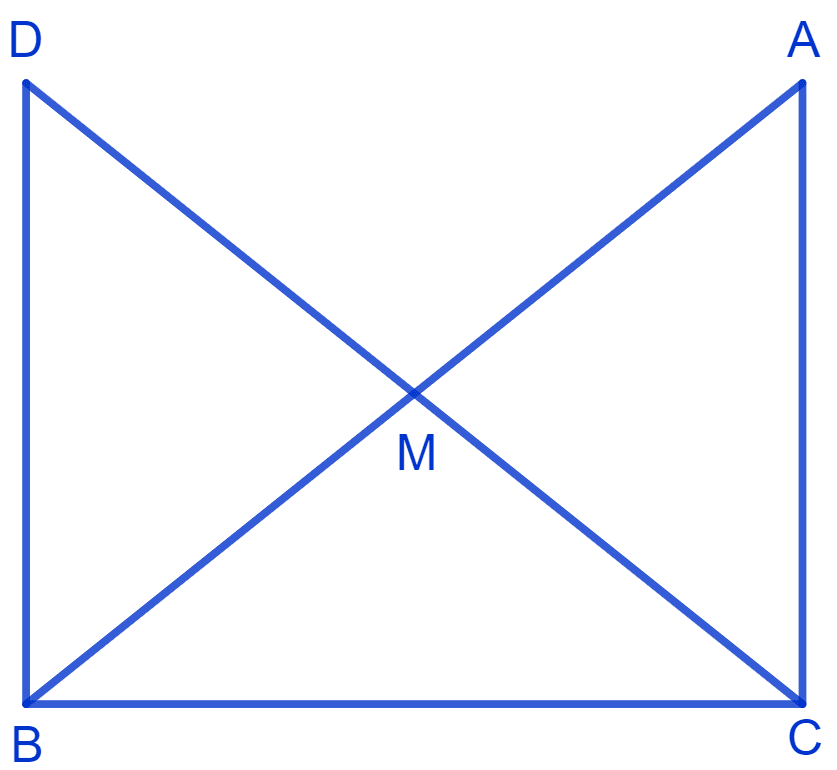
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. Show that :
(i) Δ AMC ≅ Δ BMD
(ii) ∠DBC is a right angle
(iii) Δ DBC ≅ Δ ACB
(iv) CM =
Triangles
2 Likes
Answer
(i) In Δ AMC and Δ BMD,
⇒ AM = BM (M is the mid - point of AB)
⇒ ∠AMC = ∠BMD (Vertically opposite angles are equal)
⇒ CM = DM (Given)
∴ Δ AMC ≅ Δ BMD (By S.A.S. congruence rule)
Hence, proved that Δ AMC ≅ Δ BMD.
(ii) Since,
Δ AMC ≅ Δ BMD
∴ ∠ACM = ∠BDM (By C.P.C.T.)
From figure,
∠ACM and ∠BDM are alternate interior angles. Since alternate angles are equal, it can be said that DB || AC.
We know that,
Sum of co-interior angles = 180°.
⇒ ∠DBC + ∠ACB = 180°
⇒ ∠DBC + 90° = 180° [Since, ΔACB is right angled triangle at point C]
⇒ ∠DBC = 180° - 90°
∴ ∠DBC = 90°.
Hence, proved that ∠DBC is a right angle.
(iii) Since,
Δ AMC ≅ Δ BMD
∴ DB = AC (By C.P.C.T.)
In Δ DBC and Δ ACB,
⇒ DB = AC (Proved above)
⇒ ∠DBC = ∠ACB (Both equal to 90°)
⇒ BC = CB (Common)
∴ Δ DBC ≅ Δ ACB (By S.A.S. congruence rule)
Hence, proved that Δ DBC ≅ Δ ACB.
(iv) Since,
Δ DBC ≅ Δ ACB
⇒ AB = DC (By C.P.C.T.)
⇒ =
It is given that M is the midpoint of DC
⇒ CM = =
∴ CM =
Hence, proved that CM = .
Answered By
2 Likes
Related Questions
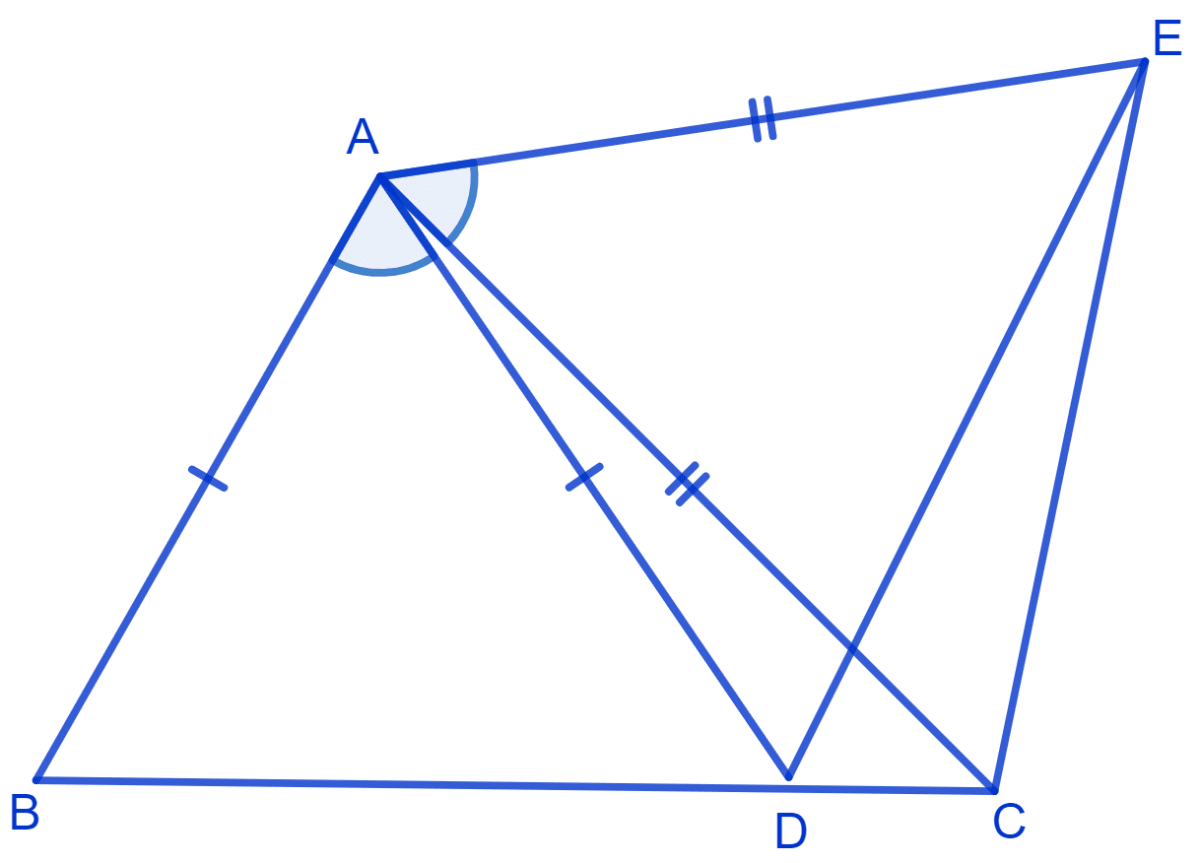
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
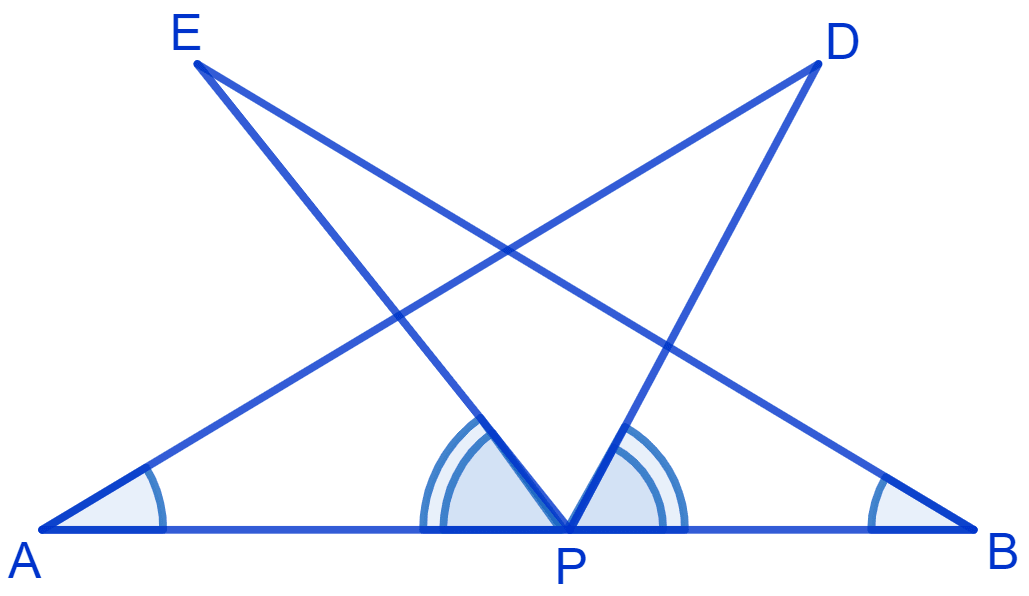
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB. Show that
(i) Δ DAP ≅ Δ EBP
(ii) AD = BE
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that :
(i) OB = OC
(ii) AO bisects ∠A
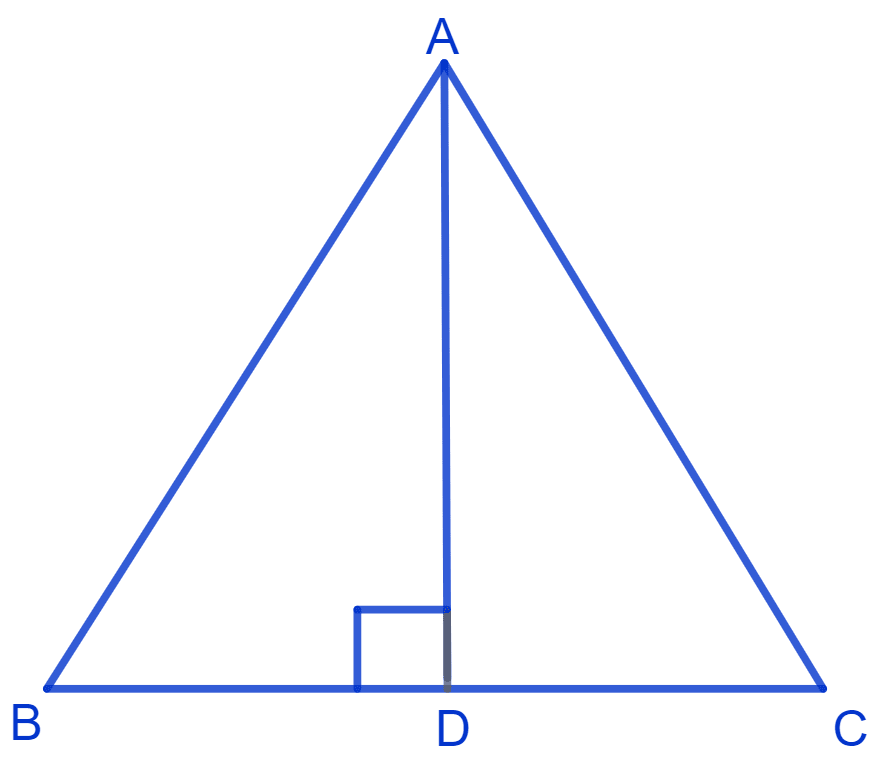
In Δ ABC, AD is the perpendicular bisector of BC. Show that Δ ABC is an isosceles triangle in which AB = AC.